El misterio de las centellas (1231)
Teoría microondas-relativistas de la centella
22 junio 2016
H.-C. Wu
Scientific Reports, volumen 6, número de artículo: 28263 (2016) | Download Citation
Resumen
Las centellas, una bola de fuego que a veces se observa durante los relámpagos, han permanecido sin explicación. Aquí presentamos una teoría integral del fenómeno: en la punta de un rayo que llega al suelo, se puede producir un grupo de electrones relativista, que a su vez excita la intensa radiación de microondas. Este último ioniza el aire local y la presión de radiación evacua el plasma resultante, formando una burbuja de plasma esférica que atrapa de manera estable la radiación. Este mecanismo se verifica mediante simulaciones de partículas. También se explican las muchas propiedades conocidas de las centellas, como el sitio de ocurrencia, la relación con los canales de rayos, la apariencia en el avión, su forma, tamaño, sonido, chispa, espectro, movimiento, así como las lesiones y daños resultantes. Nuestra teoría sugiere que las centellas pueden crearse en el laboratorio o activarse durante tormentas eléctricas. Nuestros resultados deberían ser útiles para la protección contra rayos y la seguridad de la aviación, así como para estimular el interés de la investigación en el régimen relativista de la física de microondas.
Introducción
Desde que Arago1 discutió ampliamente sobre las centellas en 1838, este extraño fenómeno natural sigue siendo un enigma. Las centellas2,3,4,5 exhiben características muy diversas, como una asociación estrecha con el rayo ordinario, una estructura globosa con brillo constante durante 1 a 5 segundos y un movimiento principalmente horizontal. Las centellas pueden formarse incluso dentro de aviones y salas cerradas, impregnar placas de vidrio, descomponerse explosivamente o en silencio, y producir sonidos y olores acre. Se han propuesto muchos modelos de centellas, pero ninguno ha sido totalmente aceptado6. En particular, estas teorías no explican la apariencia inescrutable de las centellas dentro de aviones totalmente apantallados7. Aquí, proponemos una teoría para la formación de las centellas, que puede explicar su aparición en aviones y muchas otras propiedades.
Lodge8 consideró que las centellas podrían ser excitados por una onda eléctrica estacionaria provocada por un rayo. Kapitza9 argumentó que las centellas podrían formarse a través de la ionización del aire en antinodos de ondas estacionarias electromagnéticas en el régimen de microondas. Dawson y Jones10 propusieron que una centella podría ser una burbuja de microondas confinada dentro de una capa de plasma globo. La ionización continua del aire por el microondas atrapado mantiene la capa de plasma11. Por análisis dimensional, hemos señalado12 que una burbuja de microondas puede formarse de manera similar a los solitones de luz observados en la interacción láser-plasma. Dicha burbuja de microondas contiene un modo de onda estacionaria de medio ciclo y se bosqueja en la figura 1a. El modelo de centellas tipo microondas puede explicar su penetración a través de placas de vidrio. Sin embargo, nunca se encontró el origen de la emisión de microondas de los rayos.
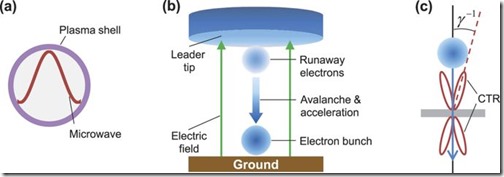 Figura 1: modelo de centella. (a) Modelo de burbuja de microondas. (b) Generación de racimos de electrones relativistas. En el último paso del líder, un grupo de electrones fuera de control emerge de la punta del líder, acelera por campos eléctricos entre el líder y la tierra, y sufre una avalancha. (c) Radiación de transición coherente (CTR) del grupo de electrones que golpea el suelo o pasa a través de las cubiertas de los aviones. γ es el factor relativista de los electrones.
Figura 1: modelo de centella. (a) Modelo de burbuja de microondas. (b) Generación de racimos de electrones relativistas. En el último paso del líder, un grupo de electrones fuera de control emerge de la punta del líder, acelera por campos eléctricos entre el líder y la tierra, y sufre una avalancha. (c) Radiación de transición coherente (CTR) del grupo de electrones que golpea el suelo o pasa a través de las cubiertas de los aviones. γ es el factor relativista de los electrones.
En este artículo, proponemos un mecanismo para la generación de microondas a partir de rayos. Como se muestra en la figura 1b, suponemos que en un evento de centellas se genera un haz de electrones relativista. Cuando este grupo toca el suelo o pasa por varios medios, se emiten potentes microondas por radiación de transición coherente (Fig. 1c). Además, verificamos que este microondas específico en plasma de aire evoluciona naturalmente en una burbuja de microondas. Estos resultados se demuestran mediante simulación de partículas en la celda (PIC) utilizando el código JPIC12.
Resultados
Manojo de electrones relativista
La suposición de racimos de electrones relativistas aislados en eventos de centellas se basa en fenómenos de alta energía13,14 descubiertos en rayos de nube a tierra. Un relámpago5 comienza con un líder negativo que se propaga hacia abajo en un proceso paso a paso con cada paso decenas de metros. Este líder escalonado tiene una corona de 1″“10 m de ancho. Moore et al.15 detectaron por primera vez > 1 MeV de radiación de un líder escalonado. Luego se observó que cada paso emite una explosión de rayos X16, que se intensifica cuando el líder se acerca al suelo. Datos recientes17 muestran que el último paso o el llamado líder estalló más cerca del suelo produce los rayos X más fuertes. Los electrones acelerados por el líder escalonado representan estos rayos X detectados, por lo que la aceleración de electrones es la más violenta en el último paso.
La fuerza de fricción del movimiento de los electrones en el aire es máxima a una energía de 100 eV, que define un campo eléctrico crítico Ec ≈ 30 MV/m14. Los campos por encima de Ecat, la punta del líder, pueden acelerar los electrones térmicos a varios keV18. Este proceso de fuga térmica19 puede producir ~ 1011 electrones. Los electrones calientes pueden ser acelerados aún más por el campo eléctrico entre la punta del líder y el suelo, y sirven como electrones semilla para sufrir una avalancha en el aire20. El flujo de electrones aumenta rápidamente como exp (z/L), donde L es la longitud de la avalancha. La energía del electrón sigue una distribución de Boltzmann exp (−ke/7.3 MeV), de modo que la energía promedio es de 7.3 MeV. El último análisis de datos21 muestra que se requieren colones de electrones relativistas para explicar los rayos X observados desde el líder escalonado, y deben estar distribuidos por Boltzmann a 7 MeV o monoenergéticos de 1 a 10 MeV.
Las ráfagas de rayos X aisladas del líder escalonado son mucho más cortas que 1 μs16. Por otro lado, las chispas de laboratorio a escala métrica en el aire pueden emitir rayos X muy similares a los de los rayos naturales. La duración de los estallidos de rayos X de las chispas de laboratorio es generalmente inferior a 10 ns23 y puede ser tan corta como 1 ns24. Se espera que los electrones acelerados tengan la misma estructura temporal que los rayos X de los rayos o chispas.
En consecuencia, se puede esperar que el último paso del líder genere un grupo de electrones relativistas espacialmente bien definidos en un evento de centella (ver Fig. 1b). Para simplificar, suponemos que este grupo tiene un perfil de densidad nb = nb0 exp (−r2/2σ2), donde nb0 es la densidad máxima y σ es el radio característico. Tomamos un tamaño de grupo (≃4σ) de decenas de cm, es decir, ~ 1 ns de duración. Como se discutió más adelante, un grupo con un número total de electrones Nb = (2Ï€)3/2nb0σ3 ≈ 1014 conducirá a una burbuja de microondas. En el mecanismo de avalancha, esto necesitaría una trayectoria de avalancha de 7L, correspondiente a una tasa de multiplicación de exp (7) ≈ 103. La longitud de avalancha L es de 7 a 30 cm cerca del suelo14 y debería soportar la rápida amplificación de estos racimos de nanosegundos. Otro mecanismo25 predice que el líder puede generar directamente ~ 1016 electrones energéticos en una escala de tiempo de 1 ns sin avalancha.
Generación de microondas
La radiación de transición se genera a partir de superficies medianas cuando un electrón entra o sale26 y puede ser coherente para un grupo de electrones aislado27. A medida que el grupo de electrones alcanza energías relativistas, sus propios campos son predominantemente transversales, es decir, Eb ≃ cBb28, que está muy cerca de una onda electromagnética. En este caso, la radiación de transición coherente puede considerarse como la onda reflejada del campo de racimo desde la superficie media29. Por lo tanto, podemos escribir la energía de radiación como ![]() donde
donde ![]() es la fórmula de reflexión de Fresnel, Wb, se transfiere a la energía de campo total del racimo, y ε es la permitividad media. La radiación es más fuerte para un metal o conductor perfecto donde ε → ∞ y â„› ≈ 1 en la región de microondas. Además, un grupo de electrones distribuidos por Boltzmann produce casi el mismo pulso de radiación de transición que uno monoenergético30.
es la fórmula de reflexión de Fresnel, Wb, se transfiere a la energía de campo total del racimo, y ε es la permitividad media. La radiación es más fuerte para un metal o conductor perfecto donde ε → ∞ y â„› ≈ 1 en la región de microondas. Además, un grupo de electrones distribuidos por Boltzmann produce casi el mismo pulso de radiación de transición que uno monoenergético30.
El panel más a la izquierda de la Fig. 2 muestra el campo transversal Eb, x de un grupo de electrones monoenergéticos de 7 MeV con σ = 4 cm, que se normaliza al pico del campo ![]() . El campo de racimo es una onda unipolar con el mismo perfil exp (−z2/2σ2) que la densidad electrónica a lo largo de la dirección del movimiento. Usando JPIC12, simulamos la radiación de transición coherente de un conductor perfecto en la Fig. 2. El campo de radiación Ex es inicialmente opuesto a Eb, x debido al límite del conductor, difracta transversalmente y evoluciona rápidamente en un pulso bipolar. Esta radiación tiene una longitud de onda central λ ≈ 7.5σ = 30 cm (es decir, 1 GHz). La rápida evolución del campo hacia la forma bipolar se debe a las pérdidas por difracción de componentes de mayor longitud de onda en un pulso unipolar31. A incidencia normal en la Fig. 2, el campo de radiación está polarizado radialmente con una distribución de intensidad en forma de anillo. La incidencia oblicua32 puede mejorar la producción de radiación y conducir a un patrón de intensidad asimétrica. Teniendo en cuenta las fluctuaciones de la superficie y los racimos no aximétricos, la radiación real podría contener solo un punto de emisión de alta intensidad, que está polarizado linealmente y hará que la formación de burbujas sea más fácil.
. El campo de racimo es una onda unipolar con el mismo perfil exp (−z2/2σ2) que la densidad electrónica a lo largo de la dirección del movimiento. Usando JPIC12, simulamos la radiación de transición coherente de un conductor perfecto en la Fig. 2. El campo de radiación Ex es inicialmente opuesto a Eb, x debido al límite del conductor, difracta transversalmente y evoluciona rápidamente en un pulso bipolar. Esta radiación tiene una longitud de onda central λ ≈ 7.5σ = 30 cm (es decir, 1 GHz). La rápida evolución del campo hacia la forma bipolar se debe a las pérdidas por difracción de componentes de mayor longitud de onda en un pulso unipolar31. A incidencia normal en la Fig. 2, el campo de radiación está polarizado radialmente con una distribución de intensidad en forma de anillo. La incidencia oblicua32 puede mejorar la producción de radiación y conducir a un patrón de intensidad asimétrica. Teniendo en cuenta las fluctuaciones de la superficie y los racimos no aximétricos, la radiación real podría contener solo un punto de emisión de alta intensidad, que está polarizado linealmente y hará que la formación de burbujas sea más fácil.
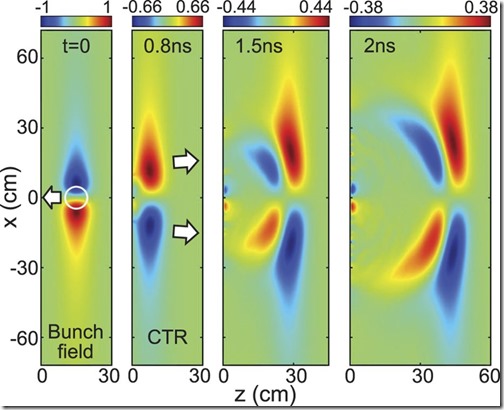 Figura 2: Resultados PIC de la generación de microondas. Distribución del campo de manojo inicial y los campos de microondas a veces 0,8 ns, 1,5 ns y 2 ns. El campo se normaliza al pico del campo de grupo Eb0. En el panel de la izquierda, el grupo se dirige hacia la superficie del plasma en z = 0. El círculo blanco marca la región del grupo con una densidad de 0.5nb0. La radiación es un reflejo del campo de racimo y se propaga a lo largo de z. Las flechas apuntan a la dirección de propagación del campo. Los parámetros se dan en el texto y los métodos.
Figura 2: Resultados PIC de la generación de microondas. Distribución del campo de manojo inicial y los campos de microondas a veces 0,8 ns, 1,5 ns y 2 ns. El campo se normaliza al pico del campo de grupo Eb0. En el panel de la izquierda, el grupo se dirige hacia la superficie del plasma en z = 0. El círculo blanco marca la región del grupo con una densidad de 0.5nb0. La radiación es un reflejo del campo de racimo y se propaga a lo largo de z. Las flechas apuntan a la dirección de propagación del campo. Los parámetros se dan en el texto y los métodos.
Formación de burbujas de microondas
Se han observado solitones láser tanto en simulaciones PIC33,34 como en experimentos35,36,37 sobre interacción relativista láser-plasma. El láser debe superar el umbral de campo relativista Er = mcω/e38 y, por lo general, es de varios ciclos. El plasma es denso con una densidad inicial n0 <nc, donde nc = ε0mω2/e2 es la densidad crítica39. Durante la propagación del láser en el plasma, el efecto de modulación autofásica40 conduce a una ampliación espectral dramática, que hace que parte de la energía del láser se desplace incluso por debajo de la frecuencia de plasma de fondo. Por lo tanto, esta parte queda atrapada en una cavidad de plasma con un modo de onda estacionaria de medio ciclo. La cavidad es esférica y se forma evacuando electrones a través de la fuerza ponderomotriz relativista41. Todo el proceso de formación toma decenas de ciclos de luz.
Aquí, discutimos la formación de burbujas para un microondas de ciclo único en la Fig. 2. El microondas debe quedar atrapado dentro de unos pocos ciclos antes de difractarse. En contraste con el mecanismo discutido anteriormente, encontramos que el plasma inicial debe ser demasiado denso con n0 ≥ nc, donde nc ≈ 1.2 × 1010cm − 3 a ω/2Ï€ = 1 GHz. La existencia de tal régimen de formación de burbujas para ondas de ciclo único indica autoconsistencia de nuestra teoría. El efecto de colisión se incluye al incorporar fricción de aire14,18 en JPIC. Lanzamos pulsos de microondas con longitud de onda λ = 30 cm en un plasma uniforme. La simulación muestra que el campo umbral requerido para la formación de burbujas es ![]()
A 1 GHz, tenemos Er ≈ 10.7 MV/my Ebl ≈ 11Er ≈ 120 MV/m, lo cual es altamente relativista. La ecuación (2) muestra claramente que el campo debe ser mayor que Ec para acelerar eficientemente los electrones y alcanzar el régimen relativista para expulsar completamente los electrones mediante la fuerza pondermotora relativista. Sorprendentemente, Er coincide con Ec para hacer posible la formación de burbujas. Aquí, verificamos los parámetros del grupo para dar el campo de umbral Ebl. Para el caso de la Fig. 2, obtenemos nb0 ≈ 3.7 × 1011cm − 3 y Nb ≈ 3.7 × 1014.
En la Fig. 3, tomamos n0 = 4nc y un campo de microondas de 310 MV/m, y dejamos t = 0 cuando el campo toca el plasma. Las instantáneas del campo de microondas y la densidad plasmática de t = 1 ns a 11 ns ilustran todo el proceso de captura automática de microondas y formación de burbujas. La presión de radiación del microondas primero empuja a los electrones a acumularse en una capa semicircular en t = 1 ns y deja una región de baja densidad en la parte trasera. A medida que la capa frontal refleja el campo, los electrones periféricos regresan a la región de baja densidad y cierran la cavidad en t at 3 ns. El campo queda atrapado y luego evoluciona a un modo de onda estacionaria. En t = 11 ns, se forma una cavidad de electrones inmóvil de unos 45 cm de profundidad en el plasma, y luego se vuelve circular y se mantiene estable después de t ≈ 15 ns. Mientras tanto, el campo de separación de carga extrae lentamente iones pesados.
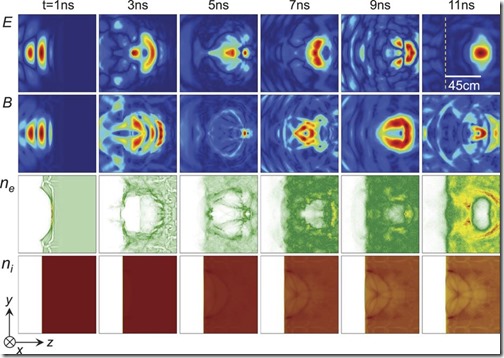 Figura 3: Resultados PIC de la captura automática de microondas y la formación de burbujas. Instantáneas del campo eléctrico de microondas E = | Ex |, campo magnético
Figura 3: Resultados PIC de la captura automática de microondas y la formación de burbujas. Instantáneas del campo eléctrico de microondas E = | Ex |, campo magnético ![]() , densidad de electrones ne y densidad de iones ni de t = 1 ns a 11 ns. La línea discontinua vertical marca la superficie del plasma. Los parámetros se dan en el texto y los métodos.
, densidad de electrones ne y densidad de iones ni de t = 1 ns a 11 ns. La línea discontinua vertical marca la superficie del plasma. Los parámetros se dan en el texto y los métodos.
En las figuras 4a, b, las instantáneas de la burbuja estable en t = 19 ns muestran que los campos adoptan un patrón de onda estacionaria de medio ciclo, los electrones se han vaciado casi por completo y los iones se han evacuado parcialmente. La fuerza electrostática entre electrones e iones está equilibrada por la presión de radiación ε0E2/4 ≈ 64 kPa, donde E = 170 MV/m es la amplitud de la onda estacionaria. La conversión periódica entre las energías eléctrica y magnética en la figura 4c confirma el modo de onda estacionaria. El campo confinado oscila en un período más largo de 1.6 ns. Este desplazamiento al rojo es causado por el efecto Doppler y la modulación de fase automática. El diámetro de la cavidad es de aproximadamente 24 cm, la mitad de la longitud de onda del campo atrapado. Para una forma de bola, la energía del campo confinado en la Fig. 4b es de aproximadamente 800J. Al ajustar el campo de microondas, la energía del campo atrapado en la burbuja oscila entre 200J y 1500J.
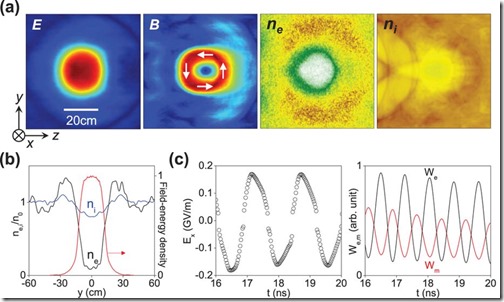 Figura 4: Resultados PIC de la burbuja estable de microondas. (a) Instantáneas del campo eléctrico de microondas E, campo magnético B, densidad de electrones ne y densidad de iones ni en t = 19 ns. Las flechas blancas marcan la dirección del campo magnético. (b) Densidad de energía de campo y densidad de plasma ne, versos y a través del centro de la burbuja. (c) Evolución del campo eléctrico, energía del campo eléctrico We y energía del campo magnético Wm en la burbuja. Los parámetros son los mismos que en la figura 3.
Figura 4: Resultados PIC de la burbuja estable de microondas. (a) Instantáneas del campo eléctrico de microondas E, campo magnético B, densidad de electrones ne y densidad de iones ni en t = 19 ns. Las flechas blancas marcan la dirección del campo magnético. (b) Densidad de energía de campo y densidad de plasma ne, versos y a través del centro de la burbuja. (c) Evolución del campo eléctrico, energía del campo eléctrico We y energía del campo magnético Wm en la burbuja. Los parámetros son los mismos que en la figura 3.
La estructura de campo tridimensional de las burbujas de microondas puede ser cercana a la de los solitones de luz observados en la simulación PIC34. Con la pérdida de energía del microondas por absorción colisión, se espera que la burbuja se convierta en un resonador de cavidad electromagnética. El modo fundamental en la frecuencia propia más baja en un resonador esférico26 es similar al de una cavidad cilíndrica28, que se asemeja a la que se muestra en la figura 4a.
Explicación de las diversas propiedades.
Las propiedades de los rayos de bola2,3,4,5 se resumen a partir de aproximadamente 5000 informes de avistamiento publicados.
Sitio de ocurrencia
Como se muestra en la Fig. 2, es necesaria una superficie plana para la generación de microondas al menos con un tamaño de centella, que puede cumplirse fácilmente en la realidad. La emisión de microondas también se ve afectada por la reflectividad del suelo ![]() . La permitividad del suelo ε aumenta con su humedad ms42. A 1 GHz, obtenemos
. La permitividad del suelo ε aumenta con su humedad ms42. A 1 GHz, obtenemos ![]() y
y ![]() , que corresponden a ≈ 25% y 56%, respectivamente. La lluvia puede conducir a ms> 60%43 y, por lo tanto, es favorable para la formación de centellas. Según lo declarado por Stenhoff4, más del 50% de los informes muestran que las precipitaciones medias o fuertes ocurren antes de la observación. Además, hay
, que corresponden a ≈ 25% y 56%, respectivamente. La lluvia puede conducir a ms> 60%43 y, por lo tanto, es favorable para la formación de centellas. Según lo declarado por Stenhoff4, más del 50% de los informes muestran que las precipitaciones medias o fuertes ocurren antes de la observación. Además, hay ![]() ≈ 65% para agua pura o de mar44. De hecho, hay 18 informes en mar2 y algunos informes sobre ríos2,4. Ciertamente, el metal tiene la mayor probabilidad de formación de bolas debido a
≈ 65% para agua pura o de mar44. De hecho, hay 18 informes en mar2 y algunos informes sobre ríos2,4. Ciertamente, el metal tiene la mayor probabilidad de formación de bolas debido a ![]() ≈ 1.
≈ 1.
Relación con los canales de rayos
El canal del rayo se refiere al golpe de retorno brillante que ocurre después de que el líder escalonado se conecta con un líder positivo que se eleva desde el suelo. El punto de partida de este líder positivo sería el punto de caída del rayo. Mostramos que las centellas son causadas por el líder escalonado, que es invisible a simple vista. El líder escalonado y su carga espejo subterránea establecen un canal oscuro para la aceleración de electrones y la avalancha. Obviamente, el sitio de formación de la pelota no está relacionado con el punto de caída del rayo. Su separación debe estar dentro de una longitud de paso de decenas de metros típicamente. Esto explica con éxito los informes en los que no se forman centellas cerca del canal de rayos o del punto de impacto4.
Aparición en aviones
Primero, la avalancha de energía electrónica de 7.3 MeV es independiente de la densidad del aire13, es decir, la altitud. Cuando un rayo cae en una aeronave, se presume que se produce el mismo grupo y entra en la aeronave con una pérdida de energía de ~ 2 MeV debido a la piel de aluminio de ~ 0.6 cm45. En segundo lugar, la radiación de transición26 no es sensible a la energía de los electrones relativistas, y su eficiencia de la superficie emergente del electrón del medio es casi la misma que el lado de reflexión discutido anteriormente. Por lo tanto, el mismo microondas intenso surgirá dentro del avión y formará una centella allí. De la misma manera, las centellas pueden aparecer en habitaciones cerradas.
Permeación a través de placas de vidrio.
Se observa que las centellas entran a las habitaciones al pasar a través de ventanas de vidrio cerradas. En experimentos de interferencia de microondas de baja potencia en la cavidad metálica46, se observa que las bolas de fuego generadas en el aire pasan a través de una placa de cerámica de 3 mm intacta. Este es un resultado directo de la capacidad del paso de microondas a través de dieléctricos. La burbuja de microondas se asemeja a una cavidad láser. Según la teoría del láser47, la onda estacionaria interna no se verá afectada si una placa de vidrio (~ 5 mm) es mucho más delgada que la longitud de onda del microondas.
Forma
A partir del análisis dimensional12, la burbuja de microondas de la Fig. 4 en realidad debería tener forma de bola como su contraparte a escala micrométrica en experimentos con plasma láser35,36,37. La captura completa del campo en la Fig. 2 puede explicar los 62 informes de centellas en forma de anillo2.
Tamaño
Las centellas tienen un diámetro común de 20″“50 cm4. Nuestra teoría muestra que el diámetro de las burbujas de microondas es aproximadamente igual a la longitud del haz de electrones en la dirección del movimiento. La longitud del grupo de decenas de cm está respaldada por la duración de los rayos X medida a partir de rayos y chispas de laboratorio, que pueden ser tan cortos como 1 ns.
Sonido
Se han reportado silbidos, zumbidos o aleteos de las centellas, lo que puede explicarse perfectamente por el efecto de audición de microondas48,49. A 0.1 mJ/cm2, un pulso de microondas (microsegundo o más corto) a 0.2″“3 GHz puede inducir una onda de sonido audible. El sonido solo puede ser escuchado por personas cuyas cabezas son irradiadas por el microondas, y ha sido descrito como un silbido, zumbido o golpeteo. Por lo tanto, las centellas pueden permanecer en silencio durante su vida útil. En el avistamiento de Jennison50, estaba a solo 0,5 m de una pelota en crucero y no informó ningún ruido.
Chispa – chispear
Las centellas a veces emiten chispas, que pueden ser causadas por la expulsión de partículas cargadas a lo largo del campo eléctrico. Especialmente, las chispas son hacia direcciones opuestas en dos informes2, lo que concuerda con la polarización lineal de la onda estacionaria en la burbuja.
Espectro
Recientemente, Cen et al.51 registraron un espectro óptico de centellas. El espectro contiene líneas de emisión de átomos en el aire y el suelo. Curiosamente, las intensidades espectrales de los átomos de O y N oscilan a 100 Hz, el doble de la frecuencia de las líneas de energía adyacentes (35 kV, 50 Hz). Este último está a solo 20 m de la pelota y puede producir un campo eléctrico de 50 Hz de ~ 1 V/cm52 en la pelota. Este campo puede inducir una deriva de electrones en la superficie de la bola en decenas de cm (ver Métodos). Este movimiento de deriva puede perturbar la emisión espectral en la cubierta de plasma. La intensidad espectral debe ser independiente de la dirección de deriva y varía a 100 Hz. La pelota está unida al suelo en una ladera, donde los electrones no pueden sentir el campo oscilante debido al efecto de detección. Por lo tanto, Si, Fe y Ca en el suelo brillan constantemente51.
Olor
El aire ionizado puede producir O3 y NO25,53, los cuales tienen un olor acre.
Decaimiento
La burbuja de microondas se descompone en silencio una vez que se agota la radiación interna. Cuando es fuertemente perturbada o perforada por un conductor, la fuga de radiación puede lanzar una onda de choque como una explosión.
Lesiones y daños.
La mayoría de las lesiones y daños reportados pueden atribuirse fácilmente a los rayos normales2,4. Sin embargo, Stenhoff4 notó que algunas quemaduras superficiales son difíciles de explicar. En el evento de Smethwick4,54, la testigo no recibió una descarga eléctrica pero sintió un calor abrasador por todas partes. Wooding55 estimó que recibió 250J de radiación ionizante de todo el cuerpo, que puede deberse a los electrones del líder escalonado y también ser responsable del enrojecimiento en sus manos y piernas. Escuchó un sonido similar a un golpeteo (traqueteo) del efecto auditivo de microondas. Sus piernas estaban adormecidas, lo que puede deberse a un daño en los nervios por el microondas a 0.1J/cm2 56. Cuando retiró la pelota con la mano, el anillo le estaba quemando el dedo. Wooding calculó que este calentamiento rápido necesitaría un microondas resonante a 1 GHz con un campo de ~ 1 MV/m, lo que concuerda bien con nuestro modelo. Otros57 informaron enrojecimiento de la piel, vómitos y pérdida de cabello, que son los resultados típicos de la radiación ionizante58. Según lo informado por X. Zhang y Q. Yan en Shanxi Daily (8 de agosto de 2014), durante una tormenta eléctrica el 5 de agosto de 2014, se vio una bola de fuego roja de 40 cm de diámetro ingresando a una oficina a través de una ventana abierta en el local Oficina de Conservación del Agua en Xinjiang, Shanxi, China. La pelota duró menos de un segundo y luego explotó ruidosamente. Cinco computadoras en la sala resultaron dañadas, lo cual es resultado directo de microondas de alta potencia56.
Movimiento
Cerca del suelo, las centellas se mueven principalmente horizontalmente a aproximadamente 2 m/s2 y generalmente viajan con el viento3. Una brisa ligera típicamente a 1.5″“3 m/s59 puede explicar esta velocidad de movimiento. Sin embargo, la convección del aire elevará la bola si los plasmas ionizados calientan el aire de fondo. Suponiendo una potencia térmica constante de 100 W, obtenemos una velocidad de convección de 23 cm/s para la bola de tamaño 30 cm (ver Métodos). Por lo tanto, el movimiento hacia arriba no es notable en comparación con el movimiento horizontal. Varios modelos2,4 especulan que la pelota podría tener una carga positiva debido a la mayor movilidad de los electrones en comparación con los iones. La bola cargada puede resistir aún más la flotabilidad o la convección del aire mediante una fuerza atractiva desde su carga espejo bajo tierra. Además, como una partícula cargada que se acelera automáticamente en una guía de ondas abierta60, la pelota puede entrar a las habitaciones a través de chimeneas.
Tiempo de vida
La vida útil típica de una centella es de 1 a 5 segundos. El análisis estadístico61 muestra que el aumento de la humedad disminuye la vida útil de la pelota, lo que puede deberse a la absorción de microondas por vapor. Los experimentos62 muestran que las bolas de fuego en el aire producidas por un microondas de 5 kW y 2,45 GHz pueden durar ~ 0,5 s después de que se apaga la fuente. Nuestra burbuja de microondas autoorganizada puede tener el mismo potencial de persistencia durante una escala de segundos. Zheng11 calculó que cientos de microondas en julios pueden mantener la capa de plasma de la burbuja durante unos segundos. Los plasmas de aire agotados continuamente por recombinación se rellenan por calentamiento por microondas. Los plasmas no neutros que se muestran en la Fig. 4b pueden resistir aún más la pérdida de recombinación.
Discusión
Se requieren experimentos para verificar nuestra teoría. Primero, formar una burbuja de microondas en el laboratorio necesitará cientos de gigavatios de microondas, que es un orden de magnitud mayor que las fuentes artificiales. Como se indica en la ref. 56, es técnicamente factible mejorar los dispositivos de microondas actuales a 100 GW. Alternativamente, uno puede adoptar un haz de electrones de alta potencia63 para simular directamente el mecanismo propuesto en la Fig. 1. Segundo, en la investigación de rayos, sugerimos detectar la radiación de microondas a GHz cerca de un punto de caída de rayos. Ya mostramos que los pares de pulsos transionosféricos del rayo son causados por el mismo mecanismo de radiación64, que proporciona una evidencia física de nuestra teoría. En los intentos de crear una centella mediante un rayo disparado por cohete65, proponemos utilizar cables sin conexión a tierra5 en lugar de cables con conexión a tierra porque se cree que las centellas solo están relacionadas con el líder escalonado. Quizás los láseres intensos pueden desencadenar relámpagos al producir un canal de plasma sin conexión a tierra cerca de las nubes de tormenta66. Para la investigación in situ de centellas, sugerimos buscar evidencia de electrones energéticos de alto flujo. Finalmente, observamos que las ondas terahercios relativistas podrían producirse a partir de electrones calientes acelerados por láser que emergen de láminas sólidas mediante radiación de transición coherente67 u ondas de plasma impulsadas por láser en el objetivo de gas68. En particular, el primer escenario está muy cerca del esquema de la Fig. 1 y puede conducir a una burbuja de radiación de terahercios a escala milimétrica.
Conclusión
En conclusión, sobre la base de una suposición razonable sobre el grupo de electrones, hemos construido una teoría autoconsistente sobre la generación de microondas y la formación de centellas. La teoría explica con éxito muchas propiedades de las centellas. Por primera vez, nos deleitamos en que las centellas son una señal de alarma de la existencia de microondas ultra fuertes y electrones abundantemente peligrosos cerca del suelo o de los aviones. Este resultado es de gran importancia para la protección contra rayos y la seguridad de la aviación. Además, se espera que nuestro trabajo estimule las actividades de investigación en física y tecnología de microondas relativistas, un área inexplorada antes.
Métodos
Análisis dimensional
La interacción de la onda electromagnética relativista y los plasmas sin colisión se rige por las ecuaciones de Maxwell y la ecuación de Lorentz relativista de electrones e iones Cuando el tiempo y el espacio se normalizan al ciclo y la longitud de onda de la onda electromagnética respectivamente, todo el sistema solo depende de dos cantidades adimensionales ![]() y
y ![]() , donde n0 es la densidad inicial del plasma, nc = ε0mω2/e2 es la densidad crítica, E0 es el campo inicial amplitud, e es la carga fundamental, m es la masa de electrones, c es la velocidad de la luz, ω es la frecuencia angular y ε0 es la permitividad al vacío. Si
, donde n0 es la densidad inicial del plasma, nc = ε0mω2/e2 es la densidad crítica, E0 es el campo inicial amplitud, e es la carga fundamental, m es la masa de electrones, c es la velocidad de la luz, ω es la frecuencia angular y ε0 es la permitividad al vacío. Si ![]() y
y ![]() son iguales para cualquier sistema con diferentes longitudes de onda λ = 2Ï€c/ω, el proceso físico debe ser idéntico en estos sistemas12. Por cierto,
son iguales para cualquier sistema con diferentes longitudes de onda λ = 2Ï€c/ω, el proceso físico debe ser idéntico en estos sistemas12. Por cierto, ![]() define el umbral de campo relativista Er = mcω/e. Para un microondas a λ = 30 cm, tenemos Er = 10.7 MV/m (Ir = 1.5 × 107W/cm2) y nc = 1.2 × 1010cm −3.
define el umbral de campo relativista Er = mcω/e. Para un microondas a λ = 30 cm, tenemos Er = 10.7 MV/m (Ir = 1.5 × 107W/cm2) y nc = 1.2 × 1010cm −3.
Simulación PIC
Todas las simulaciones se realizan con el código JPIC12, que resuelve de forma coherente las ecuaciones de Maxwell y las ecuaciones relativistas de Lorentz para electrones y iones en un espacio bidimensional. JPIC aplica un solucionador de campo libre de dispersión numérica en el eje de propagación y puede simular con precisión la dinámica de las ondas electromagnéticas de medio ciclo31. La simulación de la radiación de transición en la Fig. 2 se realiza en el plano xz. Se utiliza un plasma sobredenso para representar al conductor y su densidad tiene un efecto insignificante en los resultados. En la Fig. 2, tomamos una densidad n0 = 50nc y una resolución de 100 y 80 cuadrículas por longitud de onda (λ = 30 cm) a lo largo de los ejes z y x, respectivamente. La simulación de la formación de burbujas en las figuras 3 y 4 se realiza en el plano yz. Dado que la frecuencia de colisión en el aire es de ~ 1012Hz, es decir, miles de colisiones por ciclo, lo que hace que la resolución de colisiones individuales sea poco realista en el presente trabajo. Para la simulación, incorporamos la fuerza efectiva de fricción del aire dentro de un rango de energía electrónica [1 eV, 1 GeV]14,18 en la ecuación de electrones de Lorentz. El campo de microondas Ex es perpendicular al plano de simulación y se propaga desde un vacío a un plasma uniforme a lo largo del eje z. El pulso de microondas tiene la forma, ![]() donde E0 = 310 MV/m es la amplitud del campo, R = 9 cm es el tamaño del punto, Ï„ = 2 ns es la duración y ω/2Ï€ = 1 GHz es la frecuencia central. El ancho completo a la mitad del máximo de la envolvente de campo es Ï„/2 = 1 ns. Hay 80 y 64 cuadrículas por longitud de onda a lo largo de los ejes z e y respectivamente. Las moléculas de aire toman un peso molecular promedio de 28.97 y un estado de carga Z = 1. En la Fig. 3, para reconocer claramente la estructura de la burbuja, las barras de color se basan en valores específicos en cada momento, y por lo tanto no existe una relación cuantitativa entre los diferentes paneles.
donde E0 = 310 MV/m es la amplitud del campo, R = 9 cm es el tamaño del punto, Ï„ = 2 ns es la duración y ω/2Ï€ = 1 GHz es la frecuencia central. El ancho completo a la mitad del máximo de la envolvente de campo es Ï„/2 = 1 ns. Hay 80 y 64 cuadrículas por longitud de onda a lo largo de los ejes z e y respectivamente. Las moléculas de aire toman un peso molecular promedio de 28.97 y un estado de carga Z = 1. En la Fig. 3, para reconocer claramente la estructura de la burbuja, las barras de color se basan en valores específicos en cada momento, y por lo tanto no existe una relación cuantitativa entre los diferentes paneles.
Efectos de microondas en humanos
El microondas puede penetrar profundamente en el tejido y causar una influencia de los efectos térmicos. La audición por microondas48,49,56 es el efecto de potencia más bajo en humanos y ocurre cuando la energía absorbida en el tejido cerebral alcanza 10 μJ/g para un pulso de 10 μs. Para un cerebro adulto típico con 14 cm de diámetro y 1,4 kg de peso, obtenemos un umbral de flujo de energía de 0,1 mJ/cm2. Los experimentos48,49 muestran este efecto auditivo inducido por pulsos de microondas de 0.2″“3 GHz con 1−100 μs de duración. El análisis teórico revela que el aumento rápido de temperatura (~ μs) (~ 10−6 grados) conduce a una expansión termoelástica del tejido, que lanza una onda acústica que viaja desde el cráneo hasta el oído interno. La frecuencia de audio se encuentra en una banda audible de alta frecuencia de 7″“15 kHz, que es responsable de los sonidos de silbidos, zumbidos, golpes o clics48. Aunque bastante resistentes a la radiación ionizante69, los nervios sensoriales en el sistema nervioso periférico son particularmente sensibles al microondas70. Ocurriendo a 0.1 J/cm2 56, el daño nervioso puede conducir a un entumecimiento en las extremidades71. En nuestra teoría, el microondas alcanza ~ 1 J/cm2 para la formación de la bola, lo cual es suficiente para inducir daño auditivo y nervioso a los testigos en el microondas.
Deriva de electrones en el aire
En un campo eléctrico Ef sin (2Ï€f t) con frecuencia f, los electrones en el aire ganan una velocidad de deriva Ve = μeEf sin (2Ï€ft)13, donde μe es la movilidad de los electrones. La amplitud de la deriva de electrones es entonces ![]() . Tomando Ef = 1 V/cm, f = 50 Hz y μe = 0.6 m2/V/s18, tenemos δ ≈ 38 cm. Los iones tienen δ ≈ 0.1 mm debido a su pequeña movilidad.
. Tomando Ef = 1 V/cm, f = 50 Hz y μe = 0.6 m2/V/s18, tenemos δ ≈ 38 cm. Los iones tienen δ ≈ 0.1 mm debido a su pequeña movilidad.
Convección de aire
La burbuja de microondas calentará el aire inicialmente uniforme mediante colisiones de moléculas de electrones. Cuando la temperatura aumenta, el aire se expandirá y se elevará por flotabilidad, lo que conduce a la convección del aire. Suponiendo que el cambio de temperatura ΔT es pequeño, la velocidad de convección viene dada por ![]() 72, donde g = 9.8 m/s2 es la aceleración gravitacional, D es el tamaño de la burbuja y T0 es la temperatura inicial del aire. Si la energía térmica se transfiere principalmente por la convección del aire, uno tiene H = CpÏ0SuΔT, donde H es la potencia calorífica total de la burbuja, Cp es la capacidad calorífica específica del aire, Ï0 es la densidad del aire y S = Ï€ (D/2)2 es el área de la sección transversal de la burbuja. De estas relaciones, obtenemos
72, donde g = 9.8 m/s2 es la aceleración gravitacional, D es el tamaño de la burbuja y T0 es la temperatura inicial del aire. Si la energía térmica se transfiere principalmente por la convección del aire, uno tiene H = CpÏ0SuΔT, donde H es la potencia calorífica total de la burbuja, Cp es la capacidad calorífica específica del aire, Ï0 es la densidad del aire y S = Ï€ (D/2)2 es el área de la sección transversal de la burbuja. De estas relaciones, obtenemos 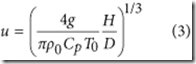
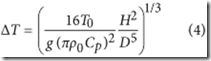
A la temperatura ambiente T0 = 293 K, tenemos Ï0 = 1.2 kg/m3 y Cp = 1 × 103J/K/kg73. Para una burbuja con D = 30 cm y H = 100 W, la velocidad de convección es u ≈ 23 cm/sy el aumento de temperatura es ΔT ≈ 5 K. También obtenemos los números de Reynolds, Peclet y Rayleigh de este sistema como 4.5 × 103, 3.2 × 103 y 1.4 × 107 respectivamente. Estos números adimensionales confirman que la convección es el mecanismo dominante del transporte de calor72.
Información Adicional
Cómo citar este artículo: Wu, H.-C. Relativistic-microwave theory of ball lightning. Sci. Rep. 6, 28263; doi: 10.1038/srep28263 (2016).
Referencias
1. 1.
Arago, F. Sur le tonnerre. Annuaire au Roi par le Bureau des Longitudes. Notices Scientifiques p. 221 (1838).
o Show contextfor reference 1
2. 2.
Singer, S. The nature of ball lightning (Plenum, New York, 1971).
o Show contextfor reference 2
3. 3.
Barry, J. D. Ball lightning and bead lightning: Extreme forms of atmospheric electricity (Plenum, New York, 1980).
o Show contextfor reference 3
4. 4.
Stenhoff, M. Ball lightning: An unsolved problem in atmospheric physics (Kluwer Academic and Plenum Publishers, New York, 1999).
o Show contextfor reference 4
5. 5.
Rakov, V. A. & Uman, M. A. Lightning: Physics and effects(Cambridge Univeristy Press, Cambridge, 2003).
o Show contextfor reference 5
6. 6.
Ball, P. First spectrum of ball lightning. Physics 7, 5 (2014).
o Show contextfor reference 6
§ Article
7. 7.
Dijkhuis, G. C. A model of ball lightning. Nature 284, 150″“151 (1980).
o Show contextfor reference 7
§ Article
8. 8.
Lodge, O. J. Lightning conductors and lightning guards (Whittaker and Co. and Bell and Sons, London, 1892).
o Show contextfor reference 8
9. 9.
Kapitza, P. L. On the nature of ball lightning. Doklady Acad. 101, 245″“248 (1955).
o Show contextfor reference 9
10. 10.
Dawson, G. A. & Jones, R. C. Ball lightning as a radiation bubble. Pure Appl. Geophys. 75, 247″“262 (1969).
o Show contextfor reference 10
§ Article
11. 11.
Zheng, X.-H. Quantitative analysis for ball lightning. Phys. Lett. A148, 463″“469 (1990).
o Show contextfor reference 11
§ Article
12. 12.
Wu, H.-C. JPIC & How to make a PIC code. Preprint at http://arxiv.org/abs/1104.3163 (2011).
o Show contextfor reference 12
13. 13.
Dwyer, J. R. & Uman, M. A. The physics of lightning. Phys. Rep. 534, 147″“241 (2014).
o Show contextfor reference 13
§ CAS
§ Article
14. 14.
Dwyer, J. R., Smith, D. M. & Cummer, S. A. High-energy atmospheric physics: Terrestrial gamma-ray flashes and related phenomena. Space Sci. Rev. 173, 133″“196 (2012).
o Show contextfor reference 14
§ CAS
§ Article
15. 15.
Moore, C. B. et al. Energetic radiation associated with lightning stepped-leaders. Geophys. Res. Lett. 28, 2141″“2144 (2001).
o Show contextfor reference 15
§ Article
16. 16.
Dwyer, J. R. et al. X-ray bursts associated with leader steps in cloud-to-ground lightning. Geophys. Res. Lett. 32, L01803 (2005).
o Show contextfor reference 16
17. 17.
Howard, J. et al. RF and X-ray source locations during the lightning attachment process. J. Geophys. Res. 115, D06204 (2010).
o Show contextfor reference 17
§ Article
18. 18.
Moss, G. D. et al. Monte Carlo model for analysis of thermal runaway electrons in streamer tips in transient luminous events and streamer zones of lightning leaders. J. Geophys. Res. 111, A02307 (2006).
o Show contextfor reference 18
§ CAS
§ Article
19. 19.
Gurevich, A. V. On the theory of runaway electrons. Sov. Phys. JETP 12, 904″“912 (1961).
o Show contextfor reference 19
20. 20.
Gurevich, A. V., Milikh, G. M. & Roussel-Dupre, R. A. Runaway electron mechanism of air breakdown and preconditioning during a thunderstorm. Phys. Lett. A 165, 463″“468 (1992).
o Show contextfor reference 20
§ CAS
§ Article
21. 21.
Babich, L. P. et al. Analysis of the experiment on registration of X-rays from the stepped leader of a cloud-to-ground lightning discharge. J. Geophys. Res. 118, 2573 (2013).
o Show contextfor reference 21
§ Article
22. 22.
Dwyer, J. R. et al. X-ray bursts produced by laboratory sparks in air. Geophys. Res. Lett. 32, L20809 (2005).
o Show contextfor reference 22
§ CAS
§ Article
23. 23.
Nguyen, C. V., J van Deursen, A. P. & Ebert, U. Multiple x-ray bursts from long discharges in air. J. Phys. D 41, 234012 (2008).
o Show contextfor reference 23
§ CAS
§ Article
24. 24.
Kochkin, P. O., J van Deursen, A. P. & Ebert, U. Experimental study on hard x-rays emitted from metre-scale negative discharges in air. J. Phys. D 48, 025205 (2015).
o Show contextfor reference 24
§ Article
25. 25.
Celestin, S. & Pasko, V. P. Energy and fluxes of thermal runaway electrons produced by exponential growth of streamers during the stepping of lightning leaders and in transient luminous events. J. Geophys. Res. 106, A03315 (2011).
o Show contextfor reference 25
26. 26.
Landau, L. D. & Lifshitz, E. M. Electrodynamics of continuous media (Pergamon, Oxford, 1984).
o Show contextfor reference 26
27. 27.
Happek, U., Sievers, A. J. & Blum, E. B. Observation of coherent transition radiation. Phys. Rev. Lett. 67, 2962″“2965 (1991).
o Show contextfor reference 27
§ CAS
§ PubMed
§ Article
28. 28.
Jackson, J. D. Classical electrodynamics (Wiley, New York, 1975).
o Show contextfor reference 28
29. 29.
Casalbuoni, S. et al. Ultrabroadband terahertz source and beamline based on coherent transition radiation. Phys. Rev. ST Accel. Beams 12, 030705 (2009).
o Show contextfor reference 29
§ CAS
§ Article
30. 30.
Tilborg, J. V. et al. Pulse shape and spectrum of coherent diffraction-limited transition radiation from electron beams. Laser Part. Beams 22, 415″“422 (2004).
o Show contextfor reference 30
31. 31.
Wu, H.-C. & Meyer-ter-Vehn, J. Giant half-cycle attosecond pulses. Nature Photon. 6, 304″“307 (2012).
o Show contextfor reference 31
§ CAS
§ Article
32. 32.
Zheng, J. et al. Theoretical study of transition radiation from hot electrons generated in the laser-solid interaction. Phys. Plasmas10, 2994″“3003 (2003).
o Show contextfor reference 32
§ CAS
§ Article
33. 33.
Naumova, N. M. et al. Formation of electromagnetic postsolitons in plasmas. Phys. Rev. Lett. 87, 185004 (2001).
o Show contextfor reference 33
§ CAS
§ Article
34. 34.
Esirkepov, T. et al. Three-dimensional relativistic electromagnetic subcycle solitons. Phys. Rev. Lett. 89, 275002 (2002).
o Show contextfor reference 34
§ CAS
§ PubMed
§ Article
35. 35.
Sarri, G. et al. Observation of plasma density dependence of electromagnetic soliton excitation by an intense laser pulse. Phys. Plasmas 18, 080704 (2011).
o Show contextfor reference 35
§ CAS
§ Article
36. 36.
Sylla, F. et al. Anticorrelation between ion acceleration and nonlinear coherent structures from laser-underdense plasma interaction. Phys. Rev. Lett. 108, 115003 (2012).
o Show contextfor reference 36
§ CAS
§ PubMed
§ Article
37. 37.
Zhu, B. et al. Observation of a strong correlation between electromagnetic soliton formation and relativistic self-focusing for ultra-short laser pulses propagating through an under-dense plasma. Phys. Plasmas 19, 102304 (2012).
o Show contextfor reference 37
§ CAS
§ Article
38. 38.
Salamina, Y. I. et al. Relativistic high-power laser-matter interactions. Phys. Rep. 427, 41″“155 (2006).
o Show contextfor reference 38
§ CAS
§ Article
39. 39.
Kruer, W. L. The physics of laser plasma interactions (Addison-Wesley Publishing Company, California, 1988).
o Show contextfor reference 39
40. 40.
Watts, I. et al. Measurements of relativistic self-phase-modulation in plasma. Phys. Rev. E 66, 036409 (2002).
o Show contextfor reference 40
§ CAS
§ Article
41. 41.
Sun, G.-Z. et al. Self-focusing of short intense pulses in plasmas. Phys. Fluids 30, 526″“532 (1987).
o Show contextfor reference 41
§ Article
42. 42.
Hallikainen, M. T. et al. Microwave dielectric behavior of wet soil-part 1: Empirical models and experimental observations. IEEE Trans. Geosci. Remote Sensing GE-23, 25″“34 (1985).
o Show contextfor reference 42
43. 43.
Xu, Q. et al. Effects of rainfall on soil moisture and water movement in a subalpine dark coniferous forest in southwestern China. Hydrol. Process. 26, 3800″“3809 (2012).
o Show contextfor reference 43
§ Article
44. 44.
Meissner, T. & Wentz, F. J. The complex dielectric constant of pure and sea water from microwave satellite observations. IEEE Trans. Geosci. Remote Sensing 42, 1836″“1849 (2004).
o Show contextfor reference 44
§ Article
45. 45.
Dwyer, J. R. et al. Estimation of the fluence of high-energy electron bursts produced by thunderclouds and the resulting radiation doses received in aircraft. J. Geophys. Res. 115, D09206 (2010).
o Show contextfor reference 45
§ Article
46. 46.
Ohtsuki, Y. H. & Ofuruton, H. Plasma fireballs formed by microwave interference in air. Nature 350, 139″“141 (1991).
o Show contextfor reference 46
§ CAS
§ Article
47. 47.
Siegman, A. E. Lasers (University Science Books, Mill Valley, CA, 1986).
o Show contextfor reference 47
48. 48.
Frey, A. H. Human auditory systems response to modulated electromagnetic energy. J. App. Physiol. 17, 689″“692 (1962).
o Show contextfor reference 48
§ CAS
49. 49.
Lin, J. C. & Wang, Z. Hearing of microwave pulses by humans and animals: Effects, mechanism, and thresholds. Health Phys. 92, 621″“628 (2007).
o Show contextfor reference 49
§ CAS
§ PubMed
§ Article
50. 50.
Jennison, R. C. Ball lightning. Nature 224, 895 (1969).
o Show contextfor reference 50
§ Article
51. 51.
Cen, J., Yuan, P. & Xue, S. Observation of the optical and spectral characteristics of ball lightning. Phys. Rev. Lett. 112, 035001 (2014).
o Show contextfor reference 51
§ CAS
§ PubMed
§ Article
52. 52.
Tzinevrakis, A., Tsanakas, D. & Mimos, E. Analytical calculation of the electric field produced by single circuit power lines with horizontal arrangement of the conductors. 51st Internationales Wissenschaftliches Kolloquium, Technische Universitaet Ilmenau. Sept. 11″“15 (2006).
o Show contextfor reference 52
53. 53.
Petit, Y. et al. Production of ozone and nitrogen oxides by laser filamentation. Appl. Phys. Lett. 97, 021108 (2010).
o Show contextfor reference 53
§ CAS
§ Article
54. 54.
Stenhoff, M. Ball lightning. Nature 260, 596″“597 (1976).
o Show contextfor reference 54
§ Article
55. 55.
Wooding, E. R. Ball lightning in Smethwick. Nature 262, 379″“380 (1976).
o Show contextfor reference 55
§ Article
56. 56.
Benford, J., Swegle, J. A. & Schamiloglu, E. High power microwaves(Taylor and Francis, New York, 2007).
o Show contextfor reference 56
57. 57.
Shmatov, M. L. Expected spectrum of high-energy photons from ball lightning. J. Plasma Phys. 72, 277″“284 (2006).
o Show contextfor reference 57
§ CAS
§ Article
58. 58.
Mettler, F. A. & Upton, A. C. Medical effects of ionizing radiation(Elsevier, USA, 2008).
o Show contextfor reference 58
59. 59.
Beaufort Scale. Royal Meteorological Society. http://www.rmets.org/weather-and-climate/observing/beaufort-scale.
o Show contextfor reference 59
60. 60.
Tyukhtin, A. V. Self-acceleration of a charge traveling into a waveguide. Phys. Rev. ST Accel. Beams 17, 021303 (2014).
o Show contextfor reference 60
§ Article
61. 61.
Amirov, A. K. & Bychkov, V. L. Observational and computer assisted analysis of data from SKB data base. Proceedings: 5th International Symposium on Ball Lightning p. 42 (1997).
o Show contextfor reference 61
62. 62.
Ofuruton, H. et al. Experimental conditions for ball lightning creation by using air gap discharge embedded in a microwave field. J. Geophys. Res. 106, 12367″“12369 (2001).
o Show contextfor reference 62
§ Article
63. 63.
Humphries, S. Charged particle beams (Dover, USA, 2013).
o Show contextfor reference 63
64. 64.
Wu, H.-C. An explanation for trans-ionospheric and sub-ionospheric pulse pairs from lightning, The 1st International Symposium on Lightning and Storm Related Phenomena (Aurillac, France, July 2″“3, 2015).
o Show contextfor reference 64
65. 65.
Hill, J. D. et al. Attempts to create ball lightning with triggered lightning. J. Atmos. Solar-Terr. Phys. 72, 913″“925 (2010).
o Show contextfor reference 65
§ Article
66. 66.
Graydon, O. & Kasparian, J. Lightning control by lasers. Nature Photon. 3, 120″“121 (2009).
o Show contextfor reference 66
§ CAS
§ Article
67. 67.
Ding, W. J., Sheng, Z. M. & Koh, W. S. High-field half-cycle terahertz radiation from relativistic laser interaction with thin solid targets. Appl. Phys. Lett. 103, 204107 (2013).
o Show contextfor reference 67
§ CAS
§ Article
68. 68.
Wu, H.-C., Sheng, Z. M. & Zhang, J. Single-cycle powerful megawatt to gigawatt terahertz pulse radiated from a wavelength-scale plasma oscillator. Phys. Rev. E 77, 046405 (2008).
o Show contextfor reference 68
§ CAS
§ Article
69. 69.
Gusev, I. A., Guskova, A. K. & Mettler, F. A. Medical management of radiation accidents. (CRC Press, Florida, 2000).
o Show contextfor reference 69
70. 70.
Sullivan, J. B. & Krieger, G. R. Clinical environmental health and toxic exposures. (Lippincott Williams & Wilkins, USA, 2001).
o Show contextfor reference 70
71. 71.
Latov, N. Peripheral neuropathy: When the numbness, weakness, and pain won»™t stop. (AAN Enterprises, USA, 2007).
o Show contextfor reference 71
72. 72.
Chenvidyakarn, T. Buoyancy effects on natural ventilation. (Cambridge University Press, Cambridge, 2013).
o Show contextfor reference 72
73. 73.
Bergman, T. L. et al. Fundamentals of heat and mass transfer. (John Wiley & Sons, USA, 2011).
o Show contextfor reference 73
Acknowledgements
This work was supported by the Thousand Youth Talents Plan, NSFC (No. 11374262), and Fundamental Research Funds for the Central Universities. We thank W. M. Wang and S. M. Weng for discussions on collisional PIC, Z. H. Wang for instruction in laser cavities, and M. Y. Yu for helpful comments.
Author information
Affiliations
1. Institute for Fusion Theory and Simulation (IFTS) and Department of Physics, Zhejiang University, Hangzhou 310027, China
o H.-C. Wu
2. IFSA Collaborative Innovation Center, Shanghai Jiao Tong University, Shanghai 200240, China
o H.-C. Wu
Competing interests
The author declares no competing financial interests.
Corresponding author
Correspondence to H.-C. Wu.
Rights and permissions
![]() This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article»™s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article»™s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Publication history
Received
25 February 2016
Accepted
02 June 2016
Published
22 June 2016
DOI