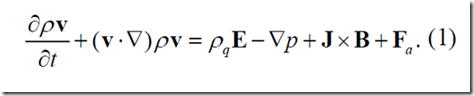Artículo de revisión

The Scientific World Journal (2006) 6, 254-278

ISSN 1537-744X; DOI 10.1100/tsw.2006.48

*Autor corresponsal

©2006 del autor.

Publicado por The Scientific World, Ltd.; www.thescientificworld.com

El enigma de la centella: Una revisión

José M. Donoso1*, José Luis Trueba2 y Antonio F. Rañada3

1Departamento de Física Aplicada, ETSI Aeronáuticos, Universidad Politécnica, 28040, Madrid, España; 2Departamento de Física Aplicada, Universidad Rey Juan Carlos, 28933 Móstoles, España; 3Departamento de Física Aplicada III, Universidad Complutense, 28040 Madrid, España

Correo electrónico: josemanuel.donoso@upm.es ; joseluis.trueba@urjc.es; afr@fis.ucm.es

Recibido el 13 de diciembre de 2005; Aceptado el 6 de febrero de 2006; Publicado el 26 de febrero de 2006

Uno de los retos científicos más intrigantes y perdurables es encontrar una explicación para las centellas, las brillantes bolas de fuego que a veces aparecen cerca de los rayos. Aunque se han propuesto muchas ideas teóricas y se ha realizado mucho trabajo experimental, aún no hay una explicación aceptada de sus sorprendentes propiedades. Son sorprendentemente estables, duran hasta 10 s, incluso minutos en algunos casos raros. Por la noche, su aspecto puede ser espectacular, pero su brillo es sólo similar al de una bombilla eléctrica doméstica. La mayoría de las veces, su movimiento es suave y horizontal, pero también puede ser errático y caótico; pueden penetrar en interiores a través de los cristales de las ventanas. Repasamos aquí algunos de los enfoques más discutidos, incluyendo tanto los modelos teóricos para encontrar una explicación como los esfuerzos experimentales para reproducirlas en el laboratorio. Distinguimos entre modelos químicos y físicos, dependiendo de si su estabilidad se basa principalmente en su composición química o en fenómenos puramente físicos relacionados con campos electromagnéticos y plasmas.

PALABRAS CLAVE: electricidad atmosférica, rayos, descargas eléctricas, física de plasmas, electromagnetismo

VISIÓN GENERAL: EL FENÓMENO

El rayo en bola (en lo sucesivo BL) es un fenómeno natural intrigante para el que, hasta el momento, no existe explicación científica; siendo, probablemente, el último fenómeno natural aún sin explicar en la baja atmósfera. Consiste en una bola llameante o bola de fuego, generalmente de color blanco brillante, rojo, naranja o amarillo, incluso azulado o verdoso, que a veces aparece cerca de la descarga de un rayo normal o, más raramente, en el aire descendiendo, casi verticalmente, de una nube. En la mayoría de los casos, se asocia a las tormentas eléctricas. Su forma suele ser esférica, pero también puede ser elipsoidal, toroidal o en forma de lágrima. En algunos casos, está rodeado de un aura o de serpentinas estrechas y coloreadas. Los BL tienden a desplazarse horizontalmente a un ritmo que los testigos suelen describir como majestuoso. Normalmente, el diámetro (óptico) oscila entre 10 y 50 cm. La distribución observada de la duración tiene un máximo entre 2 y 5 s, y un valor medio de unos 10 s o superior, con informes de más de 1 min en algunos casos. Las bolas de fuego son lo suficientemente brillantes como para verse claramente a la luz del día, siendo la potencia visible del orden de 10-150 W, similar a la de una bombilla eléctrica doméstica. Algunas bolas han aparecido dentro de aviones, desplazándose de delante hacia atrás dentro del fuselaje a lo largo del pasillo. Hay testigos que hablan de olores similares a los del ozono, azufre quemado u óxido nítrico, y de sonidos, principalmente silbidos, zumbidos o aleteos. La mayoría parece descomponerse silenciosamente, pero otras lo hacen con una explosión o una implosión. Personas y animales han muerto o resultado heridos por BL, y también se han producido incendios y daños en árboles, edificios, coches o equipos eléctricos. Esto demuestra que hay algo caliente en el interior. En estos casos, la energía liberada se ha estimado en unos 10 kJ y más de 1 MJ[1,2,3,4].

El nombre de “rayo en bola” puede inducir a error, ya que no se trata de un rayo en el sentido de una descarga eléctrica. A veces se afirma que, bajo el nombre de “relámpago de bola”, se incluyen varios fenómenos similares, pero diferentes. Un ejemplo de ello es lo que a veces se observa en los submarinos tras un cortocircuito de las baterías: aparecen bolas de plasma entre los electrodos y flotan en el aire durante varios segundos; la corriente y la energía son de unos 150 kA y 200-400 kJ. Según Stenhoff[4], BL es cualquier bola brillante o llameante señalada por testigos que no puede ser ni un rayo ordinario[5] ni un fuego de San Elmo, una aurora o cualquier otro fenómeno conocido. Presenta una extensa lista de fenómenos que pueden confundirse con BL en su excelente libro.

AB

FIGURA 1. (A) “Globo de fuego descendiendo en una habitación”. De G. Hartwig, “The Aerial World”, Londres (1886). (B) Posible centella en Basilea, Suiza (1907).

Aunque los BL se observan desde hace varios siglos, su estudio científico comenzó en el siglo XIX. Pronto quedó claro que no sería fácil encontrar una explicación; la razón principal es que, como afirmó Faraday, si son un fenómeno eléctrico, como parece lo más probable, las bolas deberían explotar casi instantáneamente, en una fracción de segundo, y su larga duración sería imposible de explicar. En parte por ello, algunos investigadores las atribuyeron a alucinaciones o delirios de los testigos presenciales, pero el consenso a favor de un fenómeno real existente es total en la actualidad. No existe, sin embargo, una teoría generalmente aceptada que pueda dar cuenta de sus propiedades. Una gran variedad de diversos modelos propuestos ha contribuido, en cierto modo, a un cierto grado de confusión. Dado que hasta ahora ha sido imposible producir BL inequívocos en el laboratorio, la investigación de este fenómeno depende, en gran medida, de los informes de testigos sin formación científica, salvo contadas excepciones. Desde la primera recopilación de este tipo de informes por Arago en 1838, se ha producido un esfuerzo cada vez mayor por compilarlos y analizarlos. Algunos programas de observación incluyen psicólogos especialistas en percepción humana para garantizar la objetividad de los relatos de los testigos.

Los informes suelen referirse al movimiento, evolución y destrucción de las bolas de fuego, no a su formación, como puede comprenderse fácilmente, ya que se observan justo después de su aparición. La búsqueda de una explicación del fenómeno es, por tanto, difícil, ya que la aparición y formación de las bolas han sido raramente descritas. Algunos científicos han establecido contactos con sociedades de montañeros, o excursionistas, pidiéndoles que informen de cualquier avistamiento de bolas de fuego y entrenándoles previamente para obtener un informe más exacto.

Este esfuerzo por encontrar datos estadísticos objetivos dio sus frutos, ya que ahora se dispone de datos cuantitativos seguros que resultan muy útiles para probar cualquier modelo teórico. En este sentido, cabe destacar dos de los resultados obtenidos. En primer lugar, se comprobó que muchas características de BL son compartidas con los rayos ordinarios, mostrando una distribución log-normal estándar para algunos parámetros típicos[6], y en segundo lugar, casi todos los eventos de BL están asociados a tormentas eléctricas. Estos dos hechos sugieren que BL es un fenómeno electromagnético. Es cierto que algunos sucesos BL han aparecido en condiciones de aire despejado sin que hubiera rayos en los alrededores, lo que se ha utilizado para apoyar modelos no electromagnéticos. Sin embargo, también se han visto rayos ordinarios fuera de situaciones de tormenta. Esto puede explicarse porque algunos rayos pueden producirse en una tormenta lejana y ser transportados por un conjunto precursor de serpentinas hasta una región despejada. En particular, éste fue el caso del “bolt from the blue” o “Gigante positivo”, un relámpago que cayó al suelo a 20 millas de la tormenta en la que se produjo, mientras que el trueno asociado sólo pudo oírse hasta unas 10 millas. No obstante, no hay que rechazar la posibilidad de que se produzca por otros efectos, como las fuerzas de fricción de un terremoto, como señalan algunos científicos.

Cualquier modelo teórico del BL debe explicar una serie de propiedades contradictorias. Según Singer[7], que estimuló de forma constante la investigación sobre BL, una teoría convincente debería explicar, al menos, las tres siguientes características distintivas de las bolas de fuego: su vida sorprendentemente larga, su movimiento flotante cerca del suelo y la forma en que desaparecen. Otra característica difícil de explicar es la capacidad de los BL para atravesar paneles de ventanas o agujeros muy pequeños y rendijas estrechas sin, aparentemente, ningún cambio en su estructura; ningún modelo da una explicación creíble de este hecho. Otro tema controvertido es si las bolas son calientes o frías, con argumentos a favor y en contra. Algunos testigos dicen que son frías ya que una bola pasó cerca de sus manos sin que sintieran calor, pero otras bolas produjeron incendios y algunas personas sufrieron quemaduras, hasta el punto de necesitar atención médica por ser heridas como por un rayo[8,9].

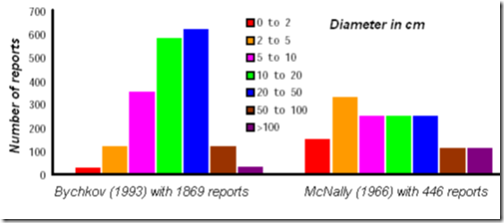FIGURA 2. Frecuencia de distribución del diámetro en dos encuestas; de Stenhoff[4].

El plan de esta revisión es el siguiente. En la siguiente sección se analizan algunos fenómenos que con frecuencia se confunden con los BL. A continuación se revisan brevemente algunos modelos teóricos, siguiendo las afirmaciones resumidas en los esquemas de clasificación sugeridos en la tercera sección. Tratamos dos tipos de modelos, según se basen en argumentos químicos o físicos; es decir, ¿los argumentos que se dan para explicar el fenómeno dependen, explícitamente, de los compuestos de materia o no? A continuación, consideramos varios experimentos que han producido estructuras brillantes que se asemejan al BL natural y seguimos con una revisión de algunos modelos recientes basados en la física del plasma. El artículo termina con un breve resumen.

CENTELLAS Y FENÓMENOS METEOROLÓGICOS APARENTEMENTE SIMILARES

Según Stenhoff, hay una gran variedad de fenómenos naturales que pueden confundirse con los BL; entre ellos, el rayo en rosario y el fuego de San Elmo son sin duda los más parecidos en su apariencia.

Relámpago en rosario

El relámpago en rosario, también llamado rayo de cuentas o en cadena, consiste en una alteración de un relámpago normal de tal forma que éste se fragmenta periódicamente a lo largo de su trayectoria, pareciendo una cadena de secciones luminosas casi esféricas que tienden a disiparse lentamente. Este fenómeno, generalmente aceptado como una forma de relámpago, o una forma de desaparición del rayo, ha sido analizado por J.D. Barry en su interesante libro[2]. La ocurrencia de relámpagos en rosario en la Naturaleza es más frecuente que la de BL, a pesar de que el número de informes referidos a los primeros es mucho menor. Esto se debe probablemente al hecho de que el comportamiento de los rayos en rosario es más regular que el de los rayos BL. Entre estos conjuntos de regularidades, destaca el hecho de que los rayos en forma de rosario suelen asociarse a rayos lineales de nube a nube que se dividen en formaciones luminosas persistentes a lo largo de la trayectoria inicial del rayo que duran aproximadamente 1-2 s. Como indica Barry, la principal característica de los rayos en forma de rosario es su aspecto punteado que a menudo se asemeja a una estructura de cuasiondas. Las formaciones luminosas de cuentas parecen decaer suavemente y sin ruido, permaneciendo cerca del canal del rayo inicial. Estas propiedades son las principales diferencias entre los fenómenos BL y los rayos en forma de rosario. Aunque la naturaleza de los relámpagos en rosario sigue siendo objeto de continua inspección, parece estar relacionada con el decaimiento del canal del rayo debido a oscilaciones longitudinales periódicas de la intensidad que dan lugar a una serie de zonas luminosas separadas por segmentos oscuros. Algunos científicos han relacionado los relámpagos en rosario con los BL, como Boichenko[10], suponiendo que ambos son plasmas débilmente ionizados (con una temperatura de unos 5,000 K) que duran hasta 1 s.

Básicamente, el plasma consiste en un sistema casi neutro de partículas cargadas eléctricamente, que interactúan entre sí y muestran un comportamiento colectivo cuya dinámica está impulsada principalmente por fuerzas electromagnéticas. Aunque podemos hablar de plasmas monoespecíficos no neutros, un estado plasmático suele estar formado por dos especies de cargas, electrones e iones, que también pueden coexistir a diferentes temperaturas en un estado termodinámico de no equilibrio, incluso en presencia de granos de polvo neutrales[11] o cargados. La naturaleza electromagnética de los rayos en rosario es comúnmente aceptada y, de hecho, lo más probable es que este fenómeno se deba a un efecto de autopellizco irregular en la corriente del rayo que casi se corta periódicamente. El efecto pellizco tiene que ver con las fuerzas de compresión, debidas a las fuerzas de Lorentz que experimentan las cargas en movimiento en un campo magnético. Un cilindro de plasma puede confinarse mediante un campo magnético azimutal externo producido por corrientes superficiales a lo largo del eje del cilindro. Este es el efecto pellizco, por el cual un tubo de flujo tiende a contraerse[11]. La fuerza magnética Fm= q(v × B), que actúa sobre una carga q en movimiento con velocidad v en un campo magnético B, conduce a la densidad de fuerza de Lorentz J × B, que aparece en la ecuación de momento de la magnetohidrodinámica (MHD)

Aquí ? y ?_q son las densidades de masa y carga del fluido, E y B representan los campos eléctrico y magnético, p es la presión isotrópica, y F_a es cualquier densidad de fuerza adicional (como la fuerza autogravitatoria en plasmas astrofísicos y efectos de viscosidad o fricción) actuando sobre el plasma que se mueve a velocidad v. El término de fuerza de Lorentz se dirige hacia el interior en la dirección radial si B es el campo azimutal automagnético de un filamento cilíndrico de plasma, con densidad de corriente axial J. A grandes rasgos, si esta corriente se modula axialmente, esta estructura cilíndrica autogravitatoria se volvería inestable y la columna de plasma puede estrangularse a sí misma, dando lugar a una serie de perlas separadas. Las condiciones axiales irregulares en un canal de rayos pueden ser el resultado de varios efectos eléctricos y de colisión en la columna impulsados por la propagación de ondas dentro del canal de rayos. Un tratamiento riguroso requeriría el análisis del desarrollo de la modulación del canal mediante el estudio de la propagación de ondas transversales y longitudinales, tal y como señala Uman[5] y se discute en Barry[2]. Al igual que en el caso del BL, no existe una explicación ampliamente aceptada para el fenómeno del rayo en rosario.

Fuego de San Elmo

El fuego de San Elmo es una descarga luminosa de color violeta o azul que se observa en el extremo de objetos puntiagudos, como mástiles de barcos o bordes de aviones, en condiciones meteorológicas tormentosas. Normalmente, estas descargas se mantienen en reposo o tienen pequeños desplazamientos sobre un hilo metálico. Pueden explicarse como efectos electrostáticos de descargas de corona, alimentadas energéticamente por la energía asociada al campo eléctrico atmosférico. El fuego de San Elmo comparte la mayoría de las características observadas en BL; por ejemplo, ambos son objetos luminosos de forma esferoidal que aparecen en situaciones de tormenta. De hecho, varios casos de BL podrían explicarse como casos especiales del fuego de San Elmo. Sin embargo, a diferencia del fuego de San Elmo, el BL puede moverse casi libremente, sin permanecer en contacto con metales o cualquier superficie electrificada. Esta es, probablemente, la característica más sorprendente de los BL; aunque la mayor parte del tiempo siguen movimientos rectos, también presentan movimientos erráticos sin cambios apreciables de altura. Lowke ha sugerido que estos movimientos podrían deberse al efecto de corrientes eléctricas superficiales esparcidas por el suelo si un BL es una descarga eléctrica, véase más adelante.

Esto sugiere que la estructura del BL es muy probablemente electromagnética y que corrientes no estacionarias y campos magnéticos en el interior de la bola estarían implicados en la explicación de sus propiedades. En este sentido, el habitual color azul del fuego de San Elmo, explicado recientemente como un efecto del nitrógeno atmosférico ionizado, puede ser mostrado también por el BL, cuya mayor variedad de colores puede relacionarse con la ionización de varios tipos de moléculas de aire. Tales ionizaciones podrían producirse por la aceleración de cargas, resultante como efecto de la reconexión de líneas magnéticas.

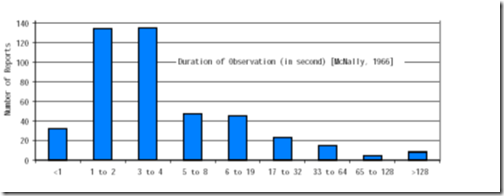FIGURA 3. Distribución por tiempo de observación, en 445 informes, a partir de datos referenciados en [4].

Las explicaciones propuestas para el rayo en rosario y el fuego de San Elmo indican claramente que los modelos electromagnéticos de BL son los mejores candidatos para modelar sus propiedades con éxito, aunque todavía queda mucho trabajo por hacer. Algunos investigadores han buscado mecanismos que puedan dar lugar a la ruptura eléctrica capaz de producir una centella. Cabe destacar el esfuerzo realizado por Prevenslik[12] para conseguir una teoría unificada de los sprites, BL y el fuego de San Elmo como cúmulos de partículas de graupel, utilizando la Teoría de Planck de la sonoluminiscencia (emisión de luz producida por sonidos) para explicar la luz radiada, aunque no se trata de un fenómeno correctamente comprendido.

CLASIFICACIÓN DE LAS CENTELLAS Y SUS MODELOS

Como ya se ha dicho, puede haber varios fenómenos diferentes que se consideren BL. Sería deseable disponer de una clasificación bien definida del BL, pero esto es difícil porque se caracteriza por muchas propiedades diferentes. Algunos científicos defienden la existencia de varios tipos de BL[4], atendiendo a su origen y fin: de rayos nube-tierra o nube-nube; flotantes libres o sujetos a conductores; procedentes de un relámpago o los que se ven en el aire, que aparecen aparentemente sin relámpagos cercanos ni tiempo tormentoso. Otro criterio distingue dos tipos de BL según su método de desaparición: disipación suave y silenciosa o explosión ruidosa. A pesar de estas dificultades, existe un consenso sobre la forma de clasificar los modelos existentes. Finkelstein y Rubinstein[13] propusieron una clasificación en dos grupos, según si la fuente de energía es interna o externa, es decir, según si la energía o la bola se almacena en el sistema desde el principio o se mantiene gracias a una fuente de energía de retroalimentación externa. En el primer grupo, hay modelos basados en plasmoides (configuraciones de equilibrio de plasmas), plasmas de alta densidad con propiedades mecánicas cuánticas, bucles cerrados de corrientes confinadas por su propio campo magnético (en algunos casos, el enlace de las corrientes desempeña un papel importante), estructuras de vórtice (como torbellinos, anillos o esferas giratorias), burbujas que contienen radiación de microondas, reacciones químicas o combustión, estructuras fractales, aerosoles, filamentos de silicio, nanotubos de carbono, procesos nucleares o nueva física, incluso miniagujeros negros primordiales. En el segundo grupo, algunos suponen que las bolas son alimentadas por descargas eléctricas o por microondas de alta frecuencia (incluso rayos cósmicos) enfocadas desde nubes de tormenta.

Un segundo esquema de clasificación de los modelos se basa en si las principales propiedades de la estructura y la producción de energía son de naturaleza química o física. Los modelos del primer tipo se basan en reacciones o compuestos químicos, como procesos de oxidación o estructuras poliméricas, siendo la composición química la responsable de la estructura o formación de la bola. Por otro lado, hay modelos que se basan en las descargas eléctricas, las propiedades de los plasmas o los fenómenos ópticos, sin hacer hincapié explícitamente en la química de las bolas. Podemos hablar, por tanto, de modelos químicos y modelos físicos. Sin embargo, nuevos desarrollos teóricos y experimentales en física y química están entrando en la tarea de encontrar una explicación adecuada a este intrigante fenómeno natural. En las secciones siguientes, consideraremos brevemente algunos de los modelos más prometedores o ampliamente discutidos, haciendo hincapié en los más recientes.

MODELOS QUÍMICOS

Desde antiguo se ha pretendido que los procesos químicos explican el BL, como los basados en reacciones químicas o en lentos procesos de combustión de materia orgánica[4]. En contra de los modelos puramente químicos se argumenta que las reacciones químicas no pueden proporcionar la alta energía que contiene el BL. Sin embargo, se han utilizado fenómenos químicos complejos para modelizar sucesos de BL, como en Turner[14], quien subraya la importancia de los procesos electroquímicos en esta tarea. Entre la gran variedad de trabajos reseñados en la monografía de Stenhoff, mencionamos aquí los primeros trabajos de Smirnov[15].

Centellas y estructuras geométricas químicas

Durante los últimos años, se han propuesto varios modelos como explicación de la larga vida y la gran energía almacenada en las bolas de fuego. Varios de ellos basan la estabilidad en configuraciones geométricas, como plasmoides filamentosos, estructuras espaciales, aerosoles cargados y fibras químicas de aerogeles poliméricos. Se han propuesto algunos modelos interesantes, que afirman la existencia de compuestos químicos adecuados para formar esqueletos cuasiestables de larga duración como soporte de BL. En 1993, Smirnov propuso que el BL podría estar compuesto por sustancias de baja densidad, formando nudos de estructuras de fibras fractales con un esqueleto rígido. Dichas estructuras, a pesar de tener la densidad de un gas, podrían estabilizarse mediante una débil distribución de la carga para alcanzar un estado de equilibrio. La energía procede de reacciones químicas y la luminosidad se debe a ondas térmicas a lo largo de las fibras, con zonas cálidas resplandecientes de unos 2000 K; los compuestos químicos excitados emiten diferentes colores en las estructuras locales moteadas. Más recientemente, en el Simposio Internacional sobre la centella de 1999 (ISBL99), Smirnov sugirió que las estructuras fractales, como el esqueleto de BL en un sistema de fibras entrelazadas, son el resultado de la interacción de un plasma con una superficie sólida.

En los últimos 2 años, la idea de estructuras esqueléticas de tamaño nanométrico también ha sido propuesta por algunos autores que defienden la existencia de estructuras filamentosas en el interior de un BL. Por ejemplo, Kukushkin[16,17] propuso que el ensamblaje de un BL como cuerpo estable se lograría mediante un híbrido de plasma y una estructura de aerogel. Algunos tipos de estas estructuras de aerogel se han obtenido en condiciones controladas en el laboratorio. Estas propiedades sugieren fuertemente que el BL podría ser un fenómeno altamente crítico, en el que pueden existir sustancias metaestables en condiciones extremas.

Oxidación de nanopartículas y estructuras de red

Abrahamson y Dinniss[18] propusieron una red de fibras formada por cadenas de partículas de tamaño nanométrico. Esta red se forma tras el impacto de un rayo en el suelo. Las nanopartículas podrían oxidarse si contienen compuestos metálicos. La aparición del resplandor y la liberación de energía del BL estarían relacionadas con estos procesos de oxidación. Para apoyar su modelo, se realizaron algunos experimentos de laboratorio[19], relacionados con la producción natural de fulguritas (formaciones vítreas causadas por impactos de rayos en la arena) y con las condiciones para formar cadenas de agregados de partículas. Las estructuras de cadena abierta observadas se justifican utilizando la fuerza de atracción entre dipolos eléctricos permanentes bajo algunas condiciones estrictas. Entre estas condiciones, se requieren concentraciones gaseosas bajas especificadas de iones para evitar el apantallamiento del dipolo local, así como una turbulencia suave para favorecer la mezcla con el fin de acercar los aglomerados más grandes entre sí[19]. Al extrapolar las condiciones experimentales a un contexto atmosférico, Abrahamson establece un conjunto de condiciones físicas y químicas para explicar la formación y el mantenimiento de un BL radiante, que pueden resumirse como sigue:

1. Producción de vapor metálico por el suministro de energía a altas temperaturas producidas en descargas eléctricas, calentamiento óhmico o fuerzas de fricción en un terremoto.

2. También es necesario algo de carbono, ya que la oxidación de este vapor “no debería competir fuertemente con su solidificación” en nanopartículas.

3. Ausencia de fuertes turbulencias, flujos u ondas de choque para mantener una estructura en red coherente.

Estos supuestos sustentarían un modelo teórico capaz de explicar varias características del BL, como la penetración a través de pequeñas grietas en cristales de ventanas o paredes. Debido a la flexibilidad de los filamentos de silicio, la red arrastrada por las corrientes de aire hasta la grieta podría comprimirse y reformarse al otro lado.

Tomando como premisa básica el requisito de que los rayos caigan regularmente sobre un objeto (como el suelo) que contenga metales u óxidos, la realización del modelo de Abrahamson y Dinniss puede explicarse como sigue: la reacción entre el óxido de silicio y el carbono produce silicio metálico en vapor en el calor del rayo. Después, el silicio se condensa en pequeñas esferas nanométricas que se juntan semejando largas fibras. Si el rayo excava un pequeño agujero en el suelo, que sirve de canal muy caliente, el vapor de silicio es expulsado entonces de esta cavidad en forma de anillo de vórtice que se difunde en una forma esférica incandescente. Los procesos de oxidación de la estructura continúan mientras la esfera se desplaza sobre el suelo. Esta esfera puede estar caliente y ser visible ópticamente mientras arde por la oxidación del silicio. Una representación gráfica esquemática del proceso se puede encontrar en Abrahamson[20].

Aunque este modelo en sí requiere una estricta confluencia de condiciones para llevar a cabo la formación y el mantenimiento de BL, parece plausible y bien propuesto. Este modelo tiene dos características interesantes: en primer lugar, la energía del BL se explica por la emisión debida a la oxidación completa del silicio, y en segundo lugar, no se requiere un estado de plasma después de la formación de la bola para mantener el brillo.

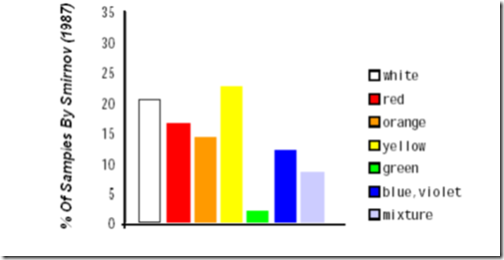FIGURA 4. Porcentajes de los colores BL más típicos, a partir de algunos datos promediados citados en Stenhoff[4].

Estructuras poliméricas

Un modelo que ha atraído cierta atención afirma que el BL puede ser una materia compuesta polimérica. En la década de 1990, Bychkov propuso que el BL podría estar compuesto por algún tipo de estructura orgánica o inorgánica similar a la forma y las propiedades de los compuestos químicos poliméricos[21,22]. Para Bychkov, un rayo puede transformar muchos materiales del entorno en fibras poliméricas que pueden enredarse formando una bola porosa. La energía puede almacenarse en la bola como resultado de la acumulación de carga eléctrica (bajo una distribución especificada) en la estructura polimérica dieléctrica enredada. El calentamiento y la luminiscencia surgirían de descargas de ruptura locales en las proximidades de las superficies cargadas de alto voltaje. Algún tipo de descarga de corona acompañada de corrientes eléctricas internas intermitentes podría explicar las emisiones de energía. Este modelo químico-físico se viene desarrollando desde hace más de 10 años. Así, en el Simposio Internacional sobre Centellas de 2004 (ISBL04), Bychkov y colaboradores ampliaron su modelo de compuesto polimérico para incluir la posibilidad de almacenamiento de alta energía a través de una bola de burbuja de carga unipolar. La burbuja cargada (con superficie fundida) podría tener una alta energía electrostática con una densidad de acumulación de energía de hasta 103 kJ/cm³. El modelo de BL como estructura polimérica-dieléctrica altamente cargada es el resultado de la agregación de polímeros naturales, como la lignina y la celulosa u otras partículas de polvo naturales. Algunos trabajos experimentales sobre descargas erosivas podrían apoyar la hipótesis de este tipo de formaciones en laboratorio. El principal problema es cómo explicar las bolas de fuego que llegan de las nubes a la Tierra con este modelo.

Los químicos también centran su atención en el papel que desempeñan el polvo y los aerosoles en la explicación del BL. Estos elementos parecen ser relevantes en otros fenómenos, como la producción de singularidades locales en los campos eléctricos que producen serpentinas líderes en los relámpagos. Los granos de polvo cargados o polarizados parecen impulsar el transporte eléctrico que rige la dinámica de los plasmas polvorientos o parcialmente ionizados. Como señaló Kikuchi[23], estos granos cargados pueden inducir procesos de autoorganización para la generación de vórtices electrodinámicos coherentes que establezcan estructuras complejas. Para subrayar la relevancia de los procesos electroquímicos y los campos locales intensos en BL, Kikuchi propuso, en el ISBL99, un método para la reproducción de un BL artificial en campos eléctricos cuspidados.

Para terminar esta sección, parece claro que la búsqueda de modelos teóricos de BL debe abordarse desde una amplia perspectiva interdisciplinar, como subraya Turner, por ejemplo. En su interesante trabajo reciente[24], Turner actualizó su propio modelo de BL basado en reacciones químicas y en la química física de los iones en el vapor de agua saturado. El modelo requiere campos eléctricos de tormenta como fuente de energía y hace uso de ideas físicas. El enigma del comportamiento del BL se entiende como el resultado de procesos electroquímicos en la superficie del plasma de aire húmedo. Más concretamente, la bola funcionaría como una “bomba de calor termoquímica alimentada por el campo eléctrico” con un núcleo central de plasma, una zona intermedia que contiene iones hidratados y la “zona de refrigeración” exterior que proporciona estabilidad mediante un equilibrio de fuerzas. Para Turner, el BL sería el resultado de un equilibrio de distintos efectos, en el que intervendrían gradientes de temperatura y presión (debidos a la composición), así como campos electromagnéticos y gravitatorios. Para explicar correctamente el BL, en el marco de la electroquímica, habría que recurrir a varias disciplinas.

MODELOS FÍSICOS

Se han propuesto muchos modelos puramente físicos desde que el físico francés Dominique F.J. Arago realizó el primer estudio de los informes sobre BL en 1838[4]. La mayoría de ellos implican campos electromagnéticos, especialmente después de que Benjamin Franklin dilucidara la naturaleza eléctrica de los rayos. Aunque algunos de los primeros modelos propuestos durante el siglo XIX son ciertamente obsoletos si se analizan bajo una perspectiva moderna, sus afirmaciones e hipótesis siguen siendo consideradas. Es el caso, por ejemplo, de los basados en estructuras de vórtice, así como la observación de Faraday en 1833 de que el BL no puede ser un fenómeno de descarga eléctrica porque decaería mucho más rápido, casi instantáneamente. En aquella época no se comprendía bien la naturaleza de las descargas eléctricas, pero su afirmación sigue siendo un obstáculo para la elaboración de modelos electromagnéticos de BL. Como en el caso de los modelos químicos, muchas de las hipótesis propuestas están en continua revisión y mejora. Algunas de ellas se comprenden mejor ahora, gracias a nuevas ideas como la autoorganización o la complejidad autoorganizada. Para un modelo que considera el BL como una estructura autoorganizada, véase, por ejemplo, Sanduloviciu y Lozneanu[25]. En particular, las consideraciones geométricas desempeñan un papel importante tanto en los modelos físicos como en los químicos.

El modelo de Kapitsa

El interés por explicar el BL se vio muy estimulado por la publicación en 1955 de un artículo de S. Kapitsa (ganador del premio Nobel de Física en 1978 por sus contribuciones a la Física de Bajas Temperaturas) en el que proponía un modelo basado en descargas electromagnéticas localizadas de alta frecuencia. Aunque se basaba en algunas ideas sugeridas previamente, el modelo atrajo mucha atención, especialmente sobre cómo producir BL en un laboratorio. Básicamente, el modelo de Kapitsa afirma que se establece una onda resonante electromagnética en la atmósfera, produciendo una localización esférica cuasi estable de cargas, bajo el supuesto de radiación electromagnética de microondas atrapada en una envoltura de plasma que se alimenta energéticamente con fuentes externas. Obtuvo una condición resonante, que depende de las dimensiones de la bola de plasma y que justifica la absorción de ondas de radio en un plasma previamente débilmente ionizado, cuyo grado de ionización aumenta al mismo tiempo que varía el volumen, hasta que se alcanza una condición resonante que relaciona la longitud de onda (aproximadamente 1 m) y el diámetro de la bola. Si la bola se calienta, una expansión destruirá la condición resonante, enfriando el plasma debido a la reducción de la absorción de energía y manteniendo una estructura estable. La propia bola debe ser un conjunto de antinodos (puntos espaciales bajo interferencia de onda constructiva total) para una onda casi estacionaria. El movimiento no convectivo sigue a los antinodos a cierta altura constante del suelo, donde el campo electromagnético emergente hace que se produzca y mantenga la bola.

Un aspecto atractivo del trabajo de Kapitsa es su explicación de la sorprendente penetración en el interior de los BL, ya que “siguen la trayectoria de oscilaciones electromagnéticas de onda corta que se propagan a través de aberturas o chimeneas conductoras tan largas como una guía de ondas”[4]. Continuó el estudio de los BL durante más de una década, relacionándolos con la emisión radioeléctrica de los rayos y las estructuras plasmáticas filamentosas que flotan en campos de alta frecuencia. A pesar del requisito de una fuente constante de onda electromagnética focalizada que no se mide en la atmósfera, el modelo de Kapitsa sugirió un gran número de experimentos con plasma de microondas que conducían a la formación de bolas de fuego plasmoides. Un ejemplo interesante de una posible realización experimental del modelo de Kapitsa puede encontrarse en el trabajo de Ohtsuki y Ofuruton[26] sobre la formación de bolas de fuego esféricas dentro de una cavidad metálica. Ofuruton creó una bola de plasma brillante y en movimiento que podía atravesar una placa de cerámica utilizando un generador de microondas de 5-kW como descarga capacitiva de 0.6-kJ. En otra simulación experimental de laboratorio de BL[27], Brandenburg y Kline produjeron algunas bolas de fuego en una cámara de microondas no resonante. Sorprendentemente, las bolas persistieron hasta 0.4 s después del apagado de las microondas.

Desde el punto de vista teórico, el modelo de Kapitsa estimuló la búsqueda de mecanismos de localización de ondas electromagnéticas. Por ejemplo, Tanaka y Tanaka[28] propusieron que BL podría ser una “localización de Anderson”. Dicha localización de un campo electromagnético podría lograrse mediante la interferencia constructiva de ondas dispersas aleatorias en medios aleatorios debido a algún tipo de resonancia estocástica. Mediante simulación numérica en el interior de un pasillo metálico de paredes irregulares, demostraron que puede producirse una intensa descarga eléctrica localizada. Situaciones similares podrían darse en un valle, en una calle, en un submarino o en el fuselaje de un avión, según afirmaron.

Modelos de plasma y el teorema de Virial

Otro modelo ampliamente discutido fue el propuesto por Finkelstein y Rubistein en 1964[13], al estudiar la posibilidad del BL plasmoidal. En su trabajo se prestó especial atención a los modelos de plasma con cargas, corrientes eléctricas y campos electromagnéticos, mientras que la materia dentro de la bola puede estar en estado estacionario, oscilatorio o turbulento. Establecieron, basándose en el teorema virial magnético, que el confinamiento de un sistema de plasma en el vacío no es posible sólo mediante campos propios debido a las leyes de conservación de la energía y el momento. Sin embargo, si hay una presión constante en el exterior de la bola, esa obstrucción desaparece, aunque existe una severa restricción a la cantidad máxima de energía almacenada; en aquel momento, se suponía que esa cantidad era del orden de 1 MJ, dos o tres órdenes de magnitud superior al contenido energético medio atribuido ahora a BL de 20-30 cm de diámetro. Esta primera estimación energética se basaba en la cantidad de agua que permanecía caliente hasta 20 min después de que BL golpeara un barril de lluvia. De nuevo, ahora sabemos que los almacenamientos de energía de 1 MJ son excepcionalmente raros.

El teorema virial, formulado por Chandrasekhar y Fermi en 1953[29] para plasmas astrofísicos, establece básicamente que la suma de las energías (gravitatoria, electromagnética y cinética del fluido) tiene que ser nula para lograr la estabilidad del sistema. En una formulación más reciente aplicada a plasmas magnetizados y utilizando la aproximación MHD, Shafranov[30] llegó a la conclusión de que, en ausencia de gravitación, las configuraciones de equilibrio acotado de los plasmas astrofísicos sólo pueden existir en presencia de determinadas distribuciones de corriente. Esto se debe a que, si la energía es positiva, el sistema se expande a menos que algunas fuerzas, como las diferencias de presión, actúen dentro de la bola. Como indicó Stenhoff[4], Shafranov sugirió que BL podría ser una estructura anular formada a partir de un rayo normal. En cualquier caso, la cuestión de si puede existir un plasmoide en el aire atmosférico abierto sigue siendo objeto de investigación y controversia. Con frecuencia se piensa que las restricciones impuestas por el teorema virial magnético son un serio impedimento para los modelos electromagnéticos de plasma de BL. Una derivación sencilla de dicho teorema puede obtenerse multiplicando ambos lados de la Ec. (1) por r e integrando sobre el volumen de plasma V limitado por una superficie S. Utilizando la ecuación de continuidad MHD ??/?t+ ? (?v) = 0, si ningún fluido sale del volumen, v dS = 0, obtenemos

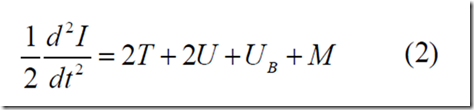para F_a = 0, que es una expresión matemática del teorema virial transitorio (dependiente del tiempo). Aquí tenemos

y

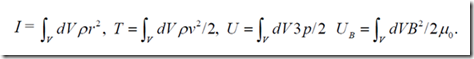I es el momento de inercia; T, U, y U_B son las energías cinética, interna y magnética. Para explorar la existencia de plasma confinado por su propio campo magnético, se hace el siguiente argumento. Si la presión p es nula fuera de V, y el campo decae más rápido que 1/r³, al permitir que la superficie de integración vaya al infinito, el término U_B produciría un aumento muy rápido de I, es decir, una explosión, ya que nada equilibraría la gran presión magnética B²/2 ?₀. Además, en un hipotético estado estacionario del plasma en el vacío, con la presión exterior p_e = 0, con F_a = 0, la relación anterior conduciría a 2T+ 2U+ U_B = 0, lo que no puede mantenerse, demostrando que el plasma no puede ser confinado por su propio campo magnético en ausencia de paredes conductoras externas. Así pues, el teorema virial excluiría cualquier modelo electromagnético de BL, a menos que exista una presión exterior p_e. Si este es el caso, tenemos que permitir que la presión sea p_e en la superficie S, para obtener

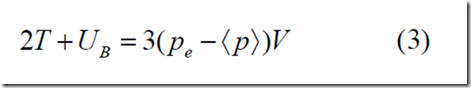para un sistema de plasma estacionario con presión media interior ?p?, inferior a p_e. Por tanto, deducimos que el almacenamiento máximo de energía no puede superar el valor de 3p_e V si se permite una depresión máxima en el interior del balón, tal y como afirman Finkelstein y Rubinstein.

Los argumentos anteriores no podrían aplicarse si el sistema se encuentra dentro de una superficie acotada. La razón es que podría haber algunos efectos de superficie que no se tienen en cuenta en la formulación anterior, que sólo se aplica a los valores medios. En algunos casos, los términos de superficie podrían dar lugar a una contribución negativa al balance energético. Esto podría ocurrir en presencia de campos eléctricos muy intensos en regiones localizadas, como en plasmas polvorientos para los que F_a ? 0, o si se viola localmente la neutralidad de la carga (?_q ? 0). Además, se pasa por alto otro caso importante en la discusión anterior. Si el campo magnético satisface J × B = 0, llamada “la condición libre de fuerza”[31], no hay efecto pellizco y todos los términos que involucran a B en la Ec. (2) desaparecen, de manera que la Ec. (3) toma la forma 2T= 3(p_e – ?p?)V, cualquiera que sea B. Obsérvese que esta relación no puede obtenerse como un caso particular de la Ec. (3), que frecuentemente se supone de validez general. Si el fluido es estacionario, v = 0, podría existir un plasma sin depresión como ocurre, por ejemplo, en un halo de polvo o humo, con la estabilidad que proporciona un campo libre de fuerzas (o de Beltrami) con altas fuerzas magnéticas cohesivas.

(A)

(B)

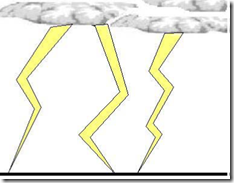
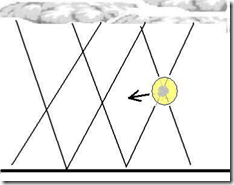
Figura 5. A) Esquema del modelo BL de Kapitsa. La bola se forma en un punto antinodo de interferencia de ondas electromagnéticas, producido tras un rayo. B) Esquema de Finkelstein y Rubinstein de un BL como una descarga incandescente con conductividad no lineal ? rodeada por una descarga Townsend. Reimpreso de la Fig. 4, con amable autorización, de D. Finkelstein y J. Rubinstein, Phys. Rev. Vol. 135, A390 (1964). Copyright (1964) de la American Physical Society.

Modelo de Finkelstein y Rubinstein

Si el modelo de Kapitsa estimuló el estudio de los aspectos experimentales del BL, Finkelstein y Rubinstein impulsaron su análisis teórico. Los sistemas plasmáticos de vida corta se habían descubierto experimentalmente tiempo atrás, y su estabilidad se debía a un campo magnético atrapado en el interior del sistema, que determina la geometría de la estructura global. Estos sistemas fueron denominados plasmoides por Bostick en 1956[4]. Aunque Finkelstein y Rubinstein[13] encontraron grandes limitaciones implicadas por el teorema virial, propusieron un posible escenario en el mismo artículo para un BL plasmoidal como una descarga localizada en un régimen de descarga Townsend mayor (alto voltaje y baja corriente).

Trataron primero la posibilidad de un modelo de plasma en presión atmosférica externa, asumiendo que en virtud del teorema de virial, un sistema de plasma no puede ser confinado por su propio campo magnético si está en el vacío, a menos que esté encerrado en un recipiente de paredes conductoras. Estimaron el tiempo de confinamiento, el campo magnético y la intensidad de corriente, asumiendo los conocidos procesos disipativos en medios ionizados. Utilizando parámetros típicos de plasma para evaluar el flujo de calor y la conductividad eléctrica, encontraron una incoherencia entre la predicción teórica para el tiempo de confinamiento ? y la vida útil comunicada del BL medio. Después, obtuvieron una relación entre la energía interna E para la bola de volumen V y la presión externa p_e, utilizando la formulación general no estacionaria del teorema virial magnético, y suponiendo que el plasma dentro de la bola está en depresión con respecto a la presión atmosférica. El plasma llenaría todo el volumen en un estado de presión isótropo. La energía resultante contenida en una bola plasmódica de 1-l no podría superar unos 100 J (a lo sumo 3p_eV en estado estacionario) con una vida útil de unos pocos microsegundos, como comprobaron experimentalmente Finkelstein y Powell unos años más tarde. Sin embargo, sugirieron la posibilidad de un plasmoide dependiente del tiempo con una conductividad no lineal dependiente de la densidad de corriente J. Se supuso que la bola de plasma se encontraba en un espacio infinito dentro de un campo eléctrico asintótico constante a gran distancia. Una posible solución daba una descarga de Townsend rodeando una descarga de resplandor esférica (voltaje y corriente intermedios), con un campo eléctrico uniforme, y continuada por un campo dipolar paralelo en la región de Townsend. La convergencia de las líneas de campo eléctrico y las corrientes en la esfera podrían mantener un estado gaseoso conductor.

Se han sugerido otras posibilidades para superar las restricciones predichas por el teorema virial. De hecho, los resultados obtenidos por Finkelstein y Rubinstein no excluyen la existencia de plasmoides de baja energía en BL. Algunos trabajos han propuesto modelos de plasma MHD para aumentar la diferencia de presión entre la bola y el aire. Por ejemplo, Wua y Oakes[32] utilizan un enfoque variacional para demostrar que la menor presión interior (y mayores gradientes de presión hacia el interior) en la atmósfera corresponde a una bola de plasma alargada. Hay que subrayar que el teorema virial no excluye la existencia de estados plasmáticos localizados de larga vida, como demostraron Faddeev y Niemi[33,34]. Además, la influencia de geometrías complejas y estructuras topológicas de campo, que pueden hacer que el estado plasmático sea altamente anisótropo, no está bien descrita por la formulación clásica del teorema virial en un espacio conectado simple. Por lo tanto, en nuestra opinión, una formulación simple del teorema virial claramente pasa por alto varias configuraciones plasmáticas interesantes que pueden existir en la Naturaleza, como indicó Bergström[35], quien conjeturó sobre la existencia de una fuerte interacción de cargas a través de la atracción dieléctrica en un medio cargado. En un medio de este tipo, la permitividad y la permeabilidad pasarían a depender del espacio, dando lugar a un campo electromagnético atractivo de Yukawa en un estado para el que no se aplica el teorema virial habitual.

Durante las últimas décadas, se han propuesto varios modelos de plasma basados en estructuras y escenarios a los que no se aplica el teorema de virial. La presencia de un núcleo sólido cargado positivamente, rodeado por una capa de plasma de electrones puros con un campo magnético atrapado en su interior, fue propuesta por Muldrew, como se menciona en Stenhoff[4]. Recientemente, Shmatov[36] ha propuesto un modelo de núcleo BL consistente en una nube de electrones e iones que oscilan entre sí. La emisión de fotones de un BL altamente energético (1 MJ) es la causa probable de las lesiones a seres humanos de las que se ha informado en algunos sucesos. También se ha propuesto la localización de vórtices electromagnéticos, efectos cuánticos, partículas de polvo cargadas y la existencia de estados plasmáticos no neutros[1,4]. En la actualidad, los estados plasmáticos no ideales pueden invocarse para buscar formulaciones generales del teorema virial clásico, permitiendo nuevos marcos teóricos para los plasmoides de larga vida que, de hecho, se han encontrado experimentalmente. En estos nuevos escenarios, dos de nosotros propusimos[37] un modelo electromagnético formado por serpentinas de plasma enlazadas y anudadas. En una línea similar, Witalis demostró en 1990[4] que el teorema virial no impide la existencia de un plasma de dos fluidos autoconfinado magnéticamente. Lo mismo podría ocurrir en un régimen de plasma anisotropizado de dos temperaturas en un campo magnético. Ambas posibilidades representan sistemas alejados del equilibrio termodinámico, donde no se aplicaría el teorema virial estático. Subrayamos que es importante seguir explorando las predicciones del MHD clásico en relación con los posibles estados del plasma. En este sentido, mencionamos el modelo BL propuesto por Kaiser y Lortz[39] en el que BL es una bola de fuego de plasma inducida por un rayo con un campo magnético decreciente en el infinito. También consideran un modelo matemático con plasma esféricamente limitado en un dominio conectado simple. Descubren que la estabilidad del plasma mejora con ligeras deformaciones de la forma esférica. Aunque aceptan honestamente que este modelo simple no puede explicar las largas vidas de BL, vale la pena investigar su solución en el marco de MHD ideal. En una línea de investigación similar, Bogoyavlenskij[40] da algunas soluciones interesantes de MHD que modelan BL.

La centella como descarga eléctrica

Otro modelo interesante y ampliamente discutido fue propuesto por Lowke en el que el BL se entiende como una descarga de corona sostenida por los campos eléctricos asociados con cargas en movimiento en la tierra tras el impacto de un rayo[41]. A diferencia del fuego de St. Elmo, aquí se propone un campo eléctrico pulsado para mantener la descarga. Este modelo de alimentación externa también ofrece una explicación de la formación, la vida útil y el movimiento de la centella. El modelo se enriquece con varios datos experimentales y calculados de campos eléctricos medidos y coeficientes de transporte para plasmas aéreos realistas. Como requisito previo, Lowke propuso que la bola se iniciara por un rayo nube-tierra que transfiere carga negativa a la tierra, mientras que la carga positiva también se transfiere a la nube en un tiempo aproximado de 1 ms, como un rayo de retorno. Las cargas negativas se mueven sobre la superficie del suelo produciendo un campo eléctrico sobre la tierra, responsable del movimiento y la potencia del BL. Tras un periodo inicial de ruptura con un campo eléctrico elevado (30 kV/cm) que produce plasma de aire, la descarga eléctrica se mantiene mediante un campo eléctrico inferior de unos 5 kV/cm, producido finalmente por la carga dispersa de 20 C que se desplaza radialmente desde 600 m. Un número reducido de electrones sirve de semilla para aumentar su densidad mediante procesos de ionización en las regiones de campo elevado antes de disminuir, debido a la unión con moléculas de oxígeno y a la recombinación con iones positivos. Dentro de la bola, el campo eléctrico impulsado por las ecuaciones de continuidad y de Poisson cambia debido a la separación de las cargas. El cálculo numérico muestra que ciertos procesos de reignición producen pulsos de corrientes que no pudieron calcularse con precisión debido a los complejos procesos de retroalimentación competitiva de la variabilidad de la temperatura y la ionización. Sin embargo, estos pulsos de corriente de aproximadamente 1 ?s podrían explicar los ruidos audibles y de radiofrecuencia, así como la producción de ozono y óxidos de nitrógeno en un aire ionizado complejo. La dispersión de cargas por el movimiento de corrientes filamentosas en el suelo sería responsable de movimientos erráticos y de la creación de una bola al otro lado del cristal de una ventana. La descomposición explosiva de la bola se produciría si la intensidad del campo eléctrico local es lo suficientemente alta como para producir descargas de arco en el interior del sistema[42]. Si bien no es capaz de reproducir todas las propiedades del BL, este modelo tiene el mérito de mostrar cómo las condiciones ambientales y la composición química del plasma pueden ser responsables del comportamiento global, y cómo los modelos electroquímicos pueden mejorarse mediante la asunción de escenarios plasmáticos.

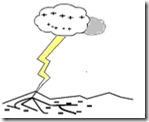
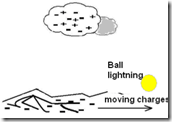FIGURA 6. Esquema del modelo BL de Lowke. La dispersión de cargas en movimiento, después de un rayo en tierra, crea un intenso campo eléctrico que sustenta el BL como una descarga de corona[41,42].

Endean[43] propuso un modelo basado en un dipolo eléctrico giratorio muy rápido con corriente neta cero. El campo eléctrico giratorio radial proporciona una contención de alta energía, superando la limitación del teorema virial ya que, para un plasmoide cargado electrostáticamente sin campo magnético, la presión eléctrica en la superficie es negativa y se relaja la restricción virial. Este modelo teórico sugiere que no hay necesidad de procesos químicos reactivos ni de sustancias estructurales.

Se puede encontrar otro modelo puramente electrostático[44,45] donde Mesenyashin modeló el BL como cáscaras multipolares cargadas electrostáticamente de moléculas de agua, formando una estructura ordenada de momentos dipolares orientados a lo largo de un campo eléctrico. Se han propuesto otros modelos electromagnéticos. Por ejemplo, Natyaganov[46] considera un BL electrocapilar, entendido como un cúmulo de vórtices esféricos tipo Hill-Taylor, o el modelo de Nikitin[47], basado en una forma de condensador de núcleo comprimido cargado con una envoltura dieléctrica, propuesto en el ISBL99.

Un modelo óptico

En ocasiones, se argumenta que la disparidad en las características del BL comunicadas indica que una explicación requeriría una nueva física. Bajo esta convicción, Torchigin[48] propuso un nuevo modelo de BL que, a primera vista, podría clasificarse como puramente óptico. Torchigin y Torchigin[49] exploran el comportamiento de una hipotética capa esférica autoconfinada de luz intensa que experimenta una reflexión interior total. La luz circula en una capa esférica de aire comprimido que funciona como una guía de ondas óptica de película fina, tras emerger de un rayo[48]. Se propagaría en el interior de la bola, como en las fibras ópticas sin revestimiento, o en el interior de esferas de vidrio de espesor reducido. Esto sería posible porque el índice de refracción sería mayor que en el aire circundante, lo que permitiría la reflexión total en las dos superficies esféricas de la envoltura. Para evitar la expansión del aire comprimido, creen que la luz intensa en el interior de la capa produce una presión de electrostricción que tiende a mantener cerca las moléculas de aire. Mientras que BL podría ser un sistema autoconsistente en el que el aire comprimido confina las ondas luminosas, la luz evita el equilibrio de presión con el aire que rodea la capa comprimida.

La presión de electrostricción ?p, inducida por la luz en un fluido, surge de la variación de la permitividad del aire ? con la densidad de masa del medio ? como

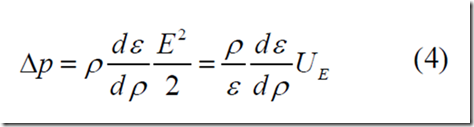donde E es la intensidad del campo eléctrico de la luz y U_E es la densidad de energía de dicho campo. El índice de refracción n, relacionado con la permitividad del vacío ?₀ como k ? ? ?₀ = n², puede aumentar con la densidad del gas ? debido a una dependencia lineal de esta magnitud con ?₀ – ?. Torchigin y Torchigin[50] revisaron el modelo y exploraron varios escenarios que podrían sostener una gran variación del índice de refracción. Encontraron que algunas de las propiedades reportadas del BL podían ser explicadas bajo las suposiciones hechas en una primera formulación del modelo. Por ejemplo, la penetración en aviones en vuelo se explica suponiendo que el BL se desplaza a lo largo de gradientes de densidad del aire hacia el lado donde la densidad es mayor. Consideran que no suele haber plasma en el BL tras su formación como consecuencia de una descarga eléctrica, donde el plasma juega un papel fundamental. A pesar de ello, no rechazan una posible capa de doble carga funcionando como condensador, como las encontradas en algunos experimentos de laboratorio que asemejan la existencia de ciertos objetos autónomos, o BL artificiales.

El efecto de los cambios de permitividad eléctrica del aire también se aplica en otros modelos. Por ejemplo, Fredkin, Mayergoyz y Zhang[51,52] aplicaron un análisis previo de objetos dieléctricos resonantes para investigar el efecto de los cambios de la permitividad eléctrica como explicación de la nucleación y formación de BL. En su explicación, la permitividad se vuelve negativa y la longitud de onda muy grande a algunas frecuencias en los objetos dieléctricos resonantes. Suponen que, en la radiación electromagnética producida por un rayo, hay frecuencias para las que la permitividad es negativa en el plasma formado. Esto permite resonancias electrostáticas que producen acumulación de energía electromagnética, visualizada como una bola de fuego. Otros modelos más exóticos, pero plausibles, invocan los átomos de Rydberg[53]. Aquí Gillman propone que el BL consiste en átomos Rydberg altamente excitados (átomos de monovalencia de estado cuántico) con grandes polarizabilidades, explicando la cohesión entre partículas como resultado de fuerzas de intercambio de fotones, en lugar de utilizar fuerzas químicas (intercambio de electrones) o efectos de campo magnético.

RELÁMPAGOS DE BOLA ARTIFICIALES

Hasta el momento, se han realizado algunas aportaciones teóricas interesantes, pero ningún modelo de BL puede explicar todas sus propiedades declaradas; la situación es similar en el ámbito experimental, ya que, aunque se han producido varias bolas de fuego en laboratorios, ninguna de ellas se acepta generalmente como una realización experimental del fenómeno real. Para una revisión de los experimentos más exitosos, como los realizados por Golka y Dijkhuis, entre otros, véase, por ejemplo, Ohtsuki[3] y Stenhoff[4]. La relación entre teoría y experimento es aquí crucial; de hecho, los modelos teóricos y los trabajos experimentales se estimulan mutuamente. En cualquier caso, el número de ideas e hipótesis teóricas supera, con mucho, las posibilidades de comprobación experimental, una situación poco satisfactoria desde el punto de vista del método científico. Esto se compensa en parte con el enorme esfuerzo dedicado al estudio minucioso de los informes de los testigos oculares. No obstante, nunca hay que olvidar el objetivo de producir una bola de fuego en condiciones físicas que puedan extrapolarse a las existentes durante las apariciones naturales de BL. Sólo una bola de fuego que muestre una gran correlación con las evidencias observacionales de campo debería llamarse BL experimental. Puede ocurrir que algunos experimentos de laboratorio, aunque ciertamente interesantes por sí mismos, no se refieran a nada parecido al BL real que aparece en la Naturaleza. Como en el caso del BL natural, varias bolas de fuego de laboratorio son poco conocidas o permanecen inexplicadas, como las llamadas capas esféricas de plasma. Estas formaciones globulares surgen en plasmas de baja presión y conductores de corriente. Pueden observarse a simple vista, fijadas a electrodos polarizados y están, probablemente, compuestas de diferentes plasmas en capas simples o múltiples[54,55].

Bolas de fuego similares, como las reportadas por Alexeff[56], pueden encontrarse en aire a presión atmosférica. Es notable que estas esferas de plasma, de varios centímetros de diámetro, persistieran hasta 0.5 s después de eliminar el suministro de la fuente de energía. El experimento muestra cómo se puede formar una bola de plasma a partir de un arco de plasma, en forma de disco, por convección ascendente. La bola de plasma consiste en una esfera de aire caliente confinada por la presión atmosférica. Se produce lentamente, para evitar ondas de choque supersónicas, con una fuente de plasma bidimensional para evitar el desarrollo de un arco lineal. Durante su formación, las pérdidas convectivas se reducen mediante la rotación de las fuentes de plasma; la radiación emitida (debida a bandas moleculares en el nitrógeno) resulta ser despreciable, si se compara con las pérdidas de energía por conducción térmica. En experimentos anteriores, Alexeff[57,58] encontró conjuntos de anillos de corriente cerrada, observados por primera vez accidentalmente en chispas de alto voltaje, afirmando que eran precursores de BL. El campo magnético autoconfinante desempeña un papel importante en estas estructuras. El alto contenido energético parece contradecir algunas estimaciones del teorema virial.

Algunos trabajos experimentales han investigado la influencia de los campos magnéticos internos en la formación de bolas de fuego, la mayoría de ellos relacionados con dispositivos de confinamiento de plasma. Koloc[59] argumentó que el BL natural puede ser una configuración de plasma estable, compartiendo varias características con los plasmas esferomak. Desgraciadamente, éstas sólo se encuentran en el laboratorio bajo condiciones controladas en cámaras de vacío a baja presión rodeadas de paredes metálicas. Sin embargo, se ha encontrado que estructuras similares de plasma de fluido frío persisten después de la supresión del campo magnético externo, como en Chen et al.[60]. Aquí Chen, Pakter y Seward encontraron, tanto teórica como experimentalmente, los equilibrios de una clase de toroides espirales de electrones autoorganizados estables que podrían explicar el BL toroidal.

Por otra parte, algunos modelos químicos teóricos han motivado el trabajo sobre bolas de fuego obtenidas a partir de descargas eléctricas que arrastran compuestos químicos o iones metálicos (denominadas descargas erosivas). Por ejemplo, Avramenko et al.[4,61] estudiaron las descargas erosivas y obtuvieron estados plasmáticos con propiedades inusuales (luminiscencia, forma esférica y tiempo de vida de 1 s) que son similares a los reportados para BL. Además, el efecto de los residuos metálicos en el tiempo de vida de un plasmoide es también de gran interés. Experimentos de este tipo también están motivados por la observación de bolas de fuego verdes de 1-s en baterías de submarinos, probablemente relacionadas con la erosión de electrodos en cortocircuitos accidentales. Dijkhuis[62], realizando experimentos con una batería submarina y corrientes de 150 kA, produjo y filmó bolas de fuego con un diámetro de 10 cm y una duración de aproximadamente 1 s. Sugirió que el fenómeno se debe a algún tipo de fuerza de intercambio mecánico-cuántico. Más recientemente, Shavanov[63] obtuvo formaciones globulares luminosas reproducibles (de unos 10 cm de diámetro, con una duración de hasta 1 s) que aparecen en descargas erosivas con los típicos colores BL. Si las bolas se tocan con un alambre metálico, expulsan alguna sustancia. Esta propiedad sugiere la existencia de un núcleo y una envoltura en los objetos, que podrían estar compuestos por dos estructuras de plasma interpenetradas. Aquí se presta especial atención a las propiedades ópticas y a la influencia de las condiciones de observación para describir los colores de las bolas. A veces, se observa que una misma bola, clasificada como perteneciente al grupo de “vida corta”, puede exhibir varios colores, con una vida útil inferior a 1 s. En opinión de Shavanov, este resultado parece confirmar la existencia de dos tipos de BL. El comportamiento óptico (incluso transparente) bajo la iluminación del flash, cuando se fotografía, es bastante diferente al observado sin el flash. Ambas observaciones están relacionadas con los colores de fondo y la percepción del color por los seres humanos, un hecho que hay que tener en cuenta en los informes de los testigos.

Un conjunto análogo de experimentos ha sido realizado por Emelin y colaboradores, otro grupo de investigación de Moscú[64,65], utilizando descargas erosivas de alto voltaje entre un ánodo en forma de anillo y un cátodo de varilla seca, ambos sumergidos en agua.

FIGURA 7. Dos bolas de fuego experimentales en una descarga erosiva por Emelin et al., una mostrando las serpentinas, la otra una cáscara. De http://balllightning.narod.ru/hvewd.html, con amable autorización.

Las esferas luminosas de 10 a 20 cm están aparentemente rodeadas por una fina película elástica que envuelve gas y, a veces, tienen una estructura filamentosa, como se muestra en la Fig. 7. Emelin et al. creen que la dispersión de metal y polímeros dentro de un pequeño volumen durante la descarga forma un modo casi crítico, dando lugar a un medio activo con una elevada energía almacenada. Un conjunto de procesos de autoorganización da lugar a los objetos autónomos. Sin embargo, sin afirmar la existencia de estructuras poliméricas complejas, Egorov y Stepanov[66] llevaron a cabo experimentos similares, estableciendo las condiciones atmosféricas necesarias para la formación natural de BL: alta actividad eléctrica y vapor de agua. Argumentan que las moléculas de agua dipolares atacan a los iones libres y rodean las partículas de polvo o aerosol. Creen que los iones hidratados (positivos y negativos) se acercan manteniendo moléculas de agua adicionales para formar agrupaciones que dan lugar a estructuras espaciales. El encadenamiento previo impediría la recombinación de cargas en un plasmoide. La energía inicial de la descarga se acumuló al formarse los pares de iones y persistió durante un largo periodo de tiempo en el plasmoide frío (330 K de temperatura).

MODELOS RECIENTES DE PLASMA

A veces se argumenta que un modelo de plasma de BL en condiciones atmosféricas no es fiable porque desaparecería en muy poco tiempo debido a la emisión de energía y a la recombinación de cargas sin fuentes externas. Esta afirmación suele relacionarse con el análisis del estado paradigmático del plasma que se encuentra en los rayos de vida corta o en los dispositivos de fusión, como los tokamaks o los stellarators. Así, a veces se olvida que el llamado “cuarto estado de la materia” es en realidad toda una variedad de estados de distintas propiedades. Van desde plasmas calientes totalmente ionizados y de alta densidad hasta plasmas metaestables superenfriados (con un alto grado de ionización incluso a baja temperatura) y plasmas astrofísicos, casi sin colisiones, a muy baja densidad. Además, en condiciones atmosféricas, el papel desempeñado por las partículas de polvo cargadas puede configurar un estado plasmático complejo (polvoriento) que podría dar lugar a nuevos escenarios plasmáticos con algunas de las propiedades señaladas para el BL. Investigaciones recientes han revelado la capacidad de generar una enorme cantidad de estructuras autoorganizadas, que comprenden plasmas cristalinos y líquidos, mediante la presencia de partículas de polvo cargadas. Este nuevo marco teórico podría decirnos mucho sobre el BL.

Algunos de los primeros modelos que tratan explícitamente esta nueva física sobre la teoría de plasmas polvorientos (complejos) pueden encontrarse en Tsytovich[67] y Smirnov[68], implicando estructuras geométricas condicionadas por la existencia de granos cargados micrométricos o nanométricos. En este contexto, y debido a la naturaleza eléctrica de muchos fenómenos atmosféricos, es razonable buscar un modelo plasmático de BL, especialmente porque una descarga de rayo es también un sistema plasmático. Obviamente, existen muchos obstáculos a la hora de construir un modelo de plasma. El principal problema en la construcción de un modelo de plasma coherente es cómo explicar qué tipo de cohesión de partículas podría conducir a un confinamiento de larga duración. Se han propuesto varios mecanismos para explicar la cohesión del plasma, pero la forma más sencilla de conseguirla es con un campo magnético. Al igual que en los dispositivos de fusión, el problema del confinamiento del plasma, por tanto, está intrínsecamente relacionado con la estructura del campo magnético aplicado y autogenerado. Para confinar el plasma, hay que confinar las líneas magnéticas y viceversa, como ocurre en los stellarators y tokamaks. Se han propuesto algunos modelos eléctricos puros para superar el problema de la cohesión de las partículas y explicar mejor otros efectos, como forma de reducir la recombinación de cargas que provocaría la extinción del plasma. La inclusión de un campo magnético es esencial, no sólo para la cohesión del plasma. Además, si se invoca un campo eléctrico puro, no podría explicarse la penetración de la bola de fuego en un avión, por ejemplo, ya que un avión es una jaula de Faraday, una pared impenetrable para la bola. En cambio, un campo magnético podría “atravesar” una pared metálica o dieléctrica, hecho que permitiría la reformación de la bola en el “otro” lado.

Modelos libre de fuerza

Además de los modelos que afirman algún tipo de reacciones nucleares, o procesos relacionados con la fusión, en algunos modelos nuevos se trata la existencia de plasmoides atmosféricos, a pesar de las restricciones del teorema virial. Tsui[69] consideró el BL como un fenómeno autoorganizado con plasma inmerso en un campo magnético esférico libre de fuerzas. Este campo, completamente alineado con la corriente del plasma en todas partes, implica que no se ejerce ninguna fuerza de pellizco sobre el plasma como se ha discutido en secciones anteriores. Una recreación experimental de este sistema, entre otros, se encuentra en un plasma esferomak que evoluciona espontáneamente a un estado libre de fuerza a partir de unas condiciones iniciales dadas. Dado que el campo no ejerce fuerza sobre aquél, debido a la nula densidad de fuerza de Lorentz, Tsui supone que el plasma está en equilibrio mecánico con el aire circundante. Tras un análisis matemático de las posibles soluciones de campo, Tsui no rechaza la existencia de campos magnéticos singulares altamente energéticos, cuya fuerza sólo se ve truncada por las limitaciones de las posibles corrientes físicas. El gran almacenamiento de energía podría ser consecuencia de la autoorganización de los vórtices magnéticos y de corriente. Una discusión más profunda de este modelo se presenta en su más reciente e interesante artículo[70]. En él, Tsui muestra que las configuraciones de campo magnético sin fuerzas, como los plasmoides atmosféricos de alta energía, no están sujetas a las restricciones del teorema virial. La razón es que el plasma está equilibrado en presión por la atmósfera, no por el propio campo magnético. La ausencia de campo eléctrico implica que no hay disipación del equilibrio magnetostático. La topología del sistema juega un papel fundamental debido a la autopreservación de la helicidad magnética h un término acuñado por primera vez por Moffatt[71,72,73,74], definido como la integral de volumen

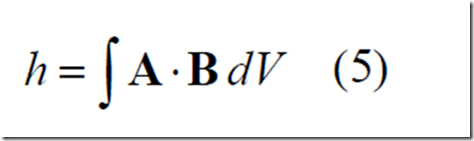donde A es el potencial vectorial magnético. La helicidad es una propiedad topológica de la configuración del campo, cuya constancia obliga al sistema a decaer a través de una cascada de estados libres de fuerza. Esto proporcionaría una vida útil de varios segundos. La configuración de plasma sin fuerzas ha sido propuesta también por Callebaut[75] en el último Simposio sobre Centellas (ISBL 2004), como una posible fase inicial de una gran clase de BL.

Un modelo topológico

Las recientes investigaciones sobre los procesos de autoorganización y filamentación en los plasmas han suscitado gran atención. La tendencia natural del plasma a autoorganizarse en estructuras filamentosas o en capas puede observarse en varios escenarios en la Naturaleza y en el laboratorio. Utilizando estas características esenciales del plasma, un modelo topológico describe el BL como un sistema de serpentinas enlazadas o anudadas que puede producirse en una descarga de rayo como resultado de procesos de autoorganización. La formación del BL sigue siendo objeto de investigación. Sin embargo, con frecuencia se admite que puede ser el resultado de un complejo conjunto de inestabilidades plasmáticas en la columna de descarga de un rayo. El modelo topológico utiliza el concepto de streamer como un canal de cargas eléctricas viajeras con estructuras plasmáticas filamentosas (neutras), portadoras de corrientes. De esta forma, nuestros streamers pueden diferir sustancialmente de los arcos, principalmente si pueden ser bucles de corrientes cerrados o anulares, posiblemente formados por el colapso de carga o corriente de una corriente cerrada previamente evolutiva y atrapada. En este modelo, la estabilidad se debe a la configuración topológica de un conjunto de serpentinas bajo líneas magnéticas enlazadas sin recurrir a estructuras sólidas. De hecho, como dijo Trubnikov[76], se pueden utilizar las herramientas teóricas habituales para explicar los procesos de filamentación en plasmas, como los bucles de corriente cerrados descubiertos recientemente[77]. Además, algunos trabajos teóricos han encontrado que algunas soluciones MHD encarnan estructuras filamentosas plasmáticas localizadas de tipo polimérico[78].

Un modelo plasmático de BL debería tener en cuenta tres observaciones:

1. La potencia emitida por un plasma del tamaño de BL es demasiado alta (1 l de plasma de aire a 15,000 K emite unos 5 MW, varios órdenes de magnitud demasiado). Esto puede ser un indicio de que la mayor parte de la bola está a temperatura ambiente, siendo sólo una pequeña fracción caliente, concentrada en estructuras filamentosas como serpentinas de corriente caliente. Si esta fracción es del orden de 1 ppm, la potencia radiada sería del orden de 10-100 W, de acuerdo con los informes de los testigos.

2. Se puede argumentar que cualquier canal de corriente de plasma en el interior de la bola sería estrangulado y cortado en muy poco tiempo por el efecto pellizco. Sin embargo, no hay efecto pinch si J × B = 0, lo que equivale a ? × B = ?B. Estos campos magnéticos libres de fuerza en el interior del plasma corresponden a estados relajados de mínima energía, como demostraron Chandrasekhar y Woltjer[79].

3. Una tercera observación se basa en el teorema virial magnético, que afirma que un sistema de cargas en interacciones electromagnéticas no tiene estado de equilibrio en ausencia de fuerzas externas porque la gran presión magnética debe producir una explosión sin ninguna otra fuerza que la compense. Sin embargo, en principio, las bolas de fuego no están en equilibrio, sino en estados metaestables de evolución lenta. Y lo que es aún más importante, la condición libre de fuerzas aniquila la presión magnética o, al menos, la reduce a un valor mucho menor si el campo está casi libre de fuerzas.

El hecho de que BL pueda contener configuraciones magnéticas de plasmas libres de fuerza es plausible. Dado que la conducción eléctrica en el aire se realiza a través de finos canales denominados serpentinas, como ocurre en los rayos ordinarios, cabe imaginar que el plasma del interior de la bola de fuego consiste en un conjunto autoorganizado de corrientes metaestables, altamente conductoras, similares a cables o corrientes de filamentos. Además, se han predicho teóricamente y observado experimentalmente estructuras filamentosas inusuales de larga vida (incluso bucles cerrados[58]) y alta densidad. Gekelman y colaboradores descubrieron estados filamentosos con una disipación mínima en un campo magnético, con canales de corriente de interacción retorcidos y sin fuerza[80]. Aquí los autores destacan el papel desempeñado por los campos magnéticos autogenerados en una dinámica impulsada por gradientes de presión de electrones, que aumentan la helicidad a medida que los canales se retuercen unos sobre otros. En el marco teórico, el problema requiere un análisis mucho más complejo de lo que se ha hecho hasta ahora; por ejemplo, hay que incluir consideraciones muy importantes, como los efectos termoquímicos y cuánticos en los procesos de transporte en el plasma, así como otros efectos no lineales. Faddeev y Niemi[33] propusieron, en el año 2000, argumentos convincentes que cuestionan ciertos puntos de vista muy extendidos sobre los plasmas. Demostraron que el teorema virial sí permite estados de equilibrio no triviales de serpentinas y campos electromagnéticos dentro de un fondo de plasma, que son “solitones topológicamente estables que describen tubos de flujo anudados y enlazados de campos magnéticos helicoidales”, como habían propuesto Rañada et al. en 1998[37,38].

El modelo topológico[81,82,83] describe BL como dos sistemas en interacción: (1) un campo magnético con sus líneas magnéticas enlazadas entre sí y (2) un conjunto de serpentinas enlazadas que contienen un plasma de aire ionizado. El modelo supone un plasma de aire ionizado confinado dentro de unas serpentinas cerradas, que llevan flujos de corriente eléctrica y un campo magnético con líneas enlazadas acopladas a las serpentinas. En la Fig. 8 se ve una representación de las serpentinas como corrientes que fluyen dentro de una bola de fuego en el modelo topológico. En este caso, dos de las seis serpentinas mostradas están unidas una vez. El plasma de aire caliente está confinado en el conjunto de serpentinas, siendo su volumen relativo pequeño, y el resto de la bola está a temperatura ambiente.

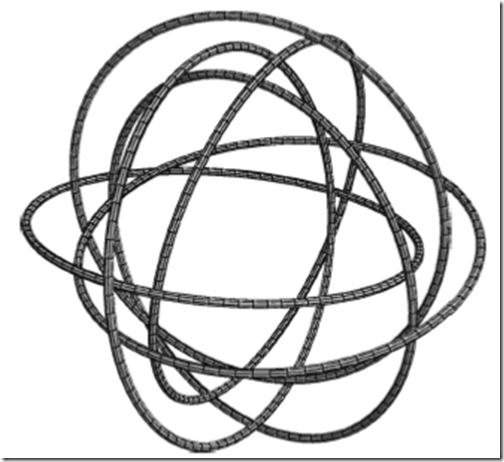FIGURA 8. Representación esquemática de las líneas magnéticas en el modelo topológico de BL. Este nudo magnético se construyó a partir del mapa de Hopf. El número de enlace de dos líneas cualesquiera es 1.

Este modelo utiliza los conceptos de nudo magnético y helicidad magnética h, Ec. (5). Un nudo magnético es un campo magnético con energía finita tal que (1) sus líneas de fuerza son cerradas, siendo las curvas de nivel de algún campo escalar complejo, y (2) el número de enlace n de estas líneas de fuerza es una constante del movimiento y no depende del par de líneas (de modo que el campo magnético tiene propiedades topológicas). Si aparece un nudo magnético B en el espacio libre, entonces su helicidad magnética puede escribirse como h = na, donde a es una constante y n es el número de enlace de las líneas magnéticas. En este modelo BL, tenemos un plasma resistivo acoplado a un nudo magnético. Utilizamos la Ec. de momento (1), acoplada a la ecuación de inducción ?B/?t= ? × (v × B), ambas en aproximación MHD de un solo fluido. Si ? es la resistividad del plasma y J la densidad de corriente eléctrica, la helicidad magnética se conserva si ?J= 0. Esta condición se cumple aproximadamente en el interior de las serpentinas, donde ? es muy pequeño, mientras que en el exterior J = 0. En otras palabras, el campo magnético es casi un nudo magnético, con propiedad topológica que estabiliza la estructura.

El modelo distingue tres etapas. La primera etapa del BL es su formación. Como ocurre en los rayos ordinarios, el aire no se conduce como un medio continuo, sino a lo largo de finos tubos de plasma altamente conductor llamados serpentinas (de unos 100 ?m de diámetro en un rayo). Cerca de una descarga de rayo ordinaria, algunas serpentinas pueden cortocircuitarse, formando bucles cerrados y enlazados. El modelo supone que se cumple la condición sin fuerza J × B = 0, de modo que las líneas de corriente y las líneas magnéticas coinciden, teniendo la misma topología: las líneas magnéticas también están cerradas y enlazadas.

En una segunda etapa, la bola de fuego sufre una relajación de Taylor muy rápida[84,85] en la que las líneas de campo magnético se rompen y se vuelven a conectar, sin cambiar la helicidad, produciendo calentamiento y aceleración de la carga. Nótese que, después de esto, no hay pérdidas mecánicas de energía, ya que la densidad de potencia v ? J × B es cero. Las pérdidas óhmicas también se minimizan para resistividades muy débiles a lo largo de las líneas de campo. El estado relajado es un nudo magnético sin fuerzas, con el valor inicial de la helicidad, que no puede disipar más energía. Si la helicidad inicial es no evanescente, entonces la estructura está muy enredada con el fluido de plasma moviéndose a lo largo de las líneas magnéticas. En consecuencia, las líneas magnéticas y las líneas de corriente pueden tener el mismo número de enlace n y esto marca el tiempo cero en BL.

La tercera etapa es la fase BL. Podríamos tener un estado estacionario después de la relajación de Taylor si despreciamos la radiación y las pérdidas resistivas. Estrictamente hablando, el sistema abierto resultante no puede estar en equilibrio porque su energía disminuye a medida que aumenta el radio de la bola, irradiando esta energía extra. Pero si la helicidad está casi conservada, este decaimiento es muy bajo, sería un estado casi quiescente, y eso explica el largo tiempo de vida. Finalmente, la bola se enfría y la conductividad disminuye, lo que lleva a la destrucción de la estructura[81].

Aunque este modelo se formuló en el MHD ideal, la investigación futura debe incluir un análisis de estabilidad y efectos disipativos. Sobre la estabilidad, podemos decir que la estabilidad global de varias estructuras de plasma puede ser asegurada para algunos estados relajados que involucran campos libres de fuerza[86]. Sobre los efectos disipativos, un estudio más profundo debería incluir el efecto de campos magnéticos fuertes que tienden a anisotropizar un sistema gobernado por dos dinámicas diferentes, paralela y transversal al campo magnético. Una amplia clase de equilibrios anisotrópicos puede derivarse a partir de soluciones MHD ideales, preservando la topología del sistema[87,88]. Cada una de estas soluciones puede ser candidata para describir el equilibrio del plasma BL. Un plasma de dos temperaturas, en el que los procesos disipativos pueden reducirse drásticamente en la dirección transversal del campo, surge de forma natural mientras que la conductividad puede ser muy alta a lo largo del campo[89]. Un análisis teórico más profundo requeriría tratar con la teoría cinética en plasmas para evaluar los coeficientes de transporte bajo altos campos electromagnéticos y gradientes de temperatura[90]. El efecto de la inhibición por el campo magnético tanto de la conducción térmica como de la difusión de la carga también sería responsable de la larga vida de BL, ya que los coeficientes de transporte transversal asociados disminuyen con la intensidad del campo magnético en función de 1/B.

El lector puede encontrar confusa la cantidad y variedad de modelos de BL. Sin embargo, BL no es el único fenómeno natural en el que se ha producido cierta controversia. Por ejemplo, es bien sabido que los streamers reportados en etapas tempranas de descargas atmosféricas pueden dividirse en ramas espontáneamente, pero cómo esta ramificación es determinada por la física subyacente ha sido materia de discusión[91,92,93].

RESUMEN

La centella es un fenómeno asombroso que sigue sin explicación tras casi dos siglos de esfuerzos científicos por dilucidar su naturaleza. Por un lado, plantea un desafío ineludible a la curiosidad y el orgullo humanos. Por otro, los intentos de encontrar una explicación a sus propiedades ofrecen interesantes perspectivas sobre el comportamiento de una serie de sistemas físicos. Suele aceptarse que los fenómenos inexplicables sólo pueden encontrarse en los ámbitos de los fenómenos muy grandes, muy pequeños o muy complejos. Las bolas de fuego no son ni grandes ni pequeñas, de hecho, se encuentran en el mesomundo y pueden no parecer muy complejas. Sin embargo, la experiencia acumulada hasta ahora sugiere que tienen, muy probablemente, una estructura realmente compleja, que toca regiones poco exploradas de la Naturaleza, como es el caso de muchos efectos inexplicables que se encuentran en los rayos ordinarios.

Las sorprendentes e intrigantes propiedades de las bolas no parecen fáciles de explicar con una simple idea. De hecho, no faltan propuestas teóricas, aunque ninguna es generalmente aceptada como la solución al enigma; en el aspecto experimental, la generación de bolas de fuego en el laboratorio ha demostrado ser una tarea difícil. Esto ha llevado a cierta confusión, ya que algunos científicos afirman que hay varios tipos de bolas bajo el mismo epígrafe, explicables en el futuro mediante diversos mecanismos físicos o químicos y que requieren enfoques y estrategias diferentes.

Existen modelos químicos y físicos. Los primeros atribuyen la estabilidad de las bolas a la química de algunos compuestos concretos, los segundos basan su estructura en el electromagnetismo o quizá en la energía nuclear. Hay argumentos de peso que apuntan a una estructura electromagnética de las bolas, aunque chocan con algunas interpretaciones del teorema virial magnético. De hecho, nadie más que el propio Faraday afirmó que una bola de fuego no puede ser un fenómeno electromagnético, ya que explotaría en una fracción de segundo. Su observación ha tenido cierta influencia negativa en los modelos electromagnéticos. Sin embargo, ahora sabemos que los sistemas electromagnéticos de plasmas, corrientes, descargas de corona, campos electromagnéticos y ondas pueden ser muy complejos y que su análisis es mucho más difícil de lo que se suponía a primera vista. Además, las conclusiones del teorema virial necesitan algunas suposiciones implícitas y no pueden ser válidas cuando hay efectos microscópicos; por ejemplo, cuando las funciones de onda pueden considerarse como un campo macroscópico (véase Faddeev y Niemi[33]).

De esta revisión pueden extraerse algunas conclusiones o sugerencias.

1. Un buen modelo teórico para las bolas de fuego debería: (1) explicar su larga vida, (2) proporcionar un mecanismo para el confinamiento de su estructura, (3) dilucidar la fuente de su energía y si es externa o interna, y (4) mostrar por qué tienden a moverse horizontalmente con algunos brotes caóticos.

2. Antes de recurrir a teorías exóticas, hay que explorar la química o la física estándar conocidas, aplicadas a nuevas estructuras no consideradas antes. En este sentido, los nuevos enfoques sobre los procesos de autoorganización podrían ser relevantes a la hora de construir un modelo adecuado.

3. Desde el punto de vista experimental, los únicos fenómenos de laboratorio que deberían considerarse auténticas BL deberían tener propiedades similares a las reportadas para las bolas de aparición natural, especialmente larga vida y luminosidad. Es especialmente importante que se produzcan en condiciones que puedan extrapolarse, según leyes de escala, al entorno atmosférico de los BL naturales.

4. Es importante “capturar” los eventos BL, es decir, observarlos in situ, donde se dice que son frecuentes, así como el entorno que los rodea. Esto nos permitiría tomar fotografías y películas con filtros y cámaras fotográficas, analizar los espectros de su radiación y medir su tamaño y vida útil, los campos electromagnéticos, las condiciones ambientales, etc. Esto no es fácil, ya que sería necesario instalar un laboratorio al aire libre para realizar observaciones continuas durante un largo periodo de tiempo, en lugares lejanos y de difícil acceso.

5. La investigación sobre BL concierne a varias disciplinas y tiene necesariamente cierto grado de interdisciplinariedad. Su marco general es la electroquímica. No hay que olvidar en este sentido que los efectos químicos desempeñan un papel en la física del plasma, por ejemplo, en los nuevos campos de los plasmas polvorientos. Además, aunque el BL es un fenómeno macroscópico, los efectos cuánticos pueden ser importantes, ya que siempre están implícitos en la física de plasmas.

AGRADECIMIENTOS

Esta investigación ha sido parcialmente financiada por el Ministerio de Ciencia y Tecnología de España, en el marco del proyecto BFM2003-05453.

REFERENCIAS

1. Singer, S. (1971) The Nature of Ball Lightning. Plenum Press, New York.

2. Barry, J.D. (1980) Ball Lightning and Bead Lightning. Plenum Press, New York.

3. Ohtsuki, Y.H., Ed. (1989) The Science of Ball Lightning. World Scientific, Singapore.

4. Stenhoff, M. (1999) Ball Lightning. An Unsolved Problem in Atmospheric Physics. Kluwer, Dordrecht.

5. Uman, M.A. (1984) Lightning. Dover, New York; (1986) All About Lightning. Dover, New York.

6. Dijkhuis, G.C. (1992) Proceedings of the Fourth TORRO Conference: Ball Lightning (Oxford). Tornado and Storm Research Organisation (TORRO), Richmond, Surrey, U.K.

7. Singer, S. (2002) Ball lightning: the scientific effort. Philos. Trans. R. Soc. Lond. A 360, 5–9.

8. Selvaggi, G., Monstrey, S., von Heimburg, D., Hamdi, M., Van Landuyt, K., and Blondeel, P. (2003) Ball lightning burn. Ann. Plast. Surg. 50, 541–544.

9. Edlich, R.F., Farinholt, H.A., Winters, K.L., Britt, L.D., and Long, W.B. (2005) Modern concepts of treatment and prevention of lightning injuries. J. Long Term Eff .Med. Implants 15, 185–196.

10. Boichenko, A.M. (1999) Ball lightning with a lifetime t < 1 s. Tech. Phys. 44, 1247

11. Sturrock, P.A. (1994) Plasma Physics. An Introducction of the Theory of Astrophysical, Geophysical and Laboratory Plasmas. Cambridge University Press.

12. Prevenslik, T. (2001) A unified theory for ‘sprites’, St. Elmo’s fire and ball lightning. J. Meteorol. 26, 204.

13. Finkelstein, D. and Rubinstein, J. (1964) Ball lightning. Phys. Rev. 135, 390.

14. Turner, D.J. (1998) Ball lightning and other meteorological phenomena. Phys. Rep. 293, 1–60.

15. Smirnov, B.M. (1987) The properties and the nature of ball lightning. Phys. Rep. 152, 177–226.

16. Kukushkin, A.B. and Rantsev-Kartinov, V.A. (2001) Observations of Long-Lived Microdust-Assembled Skeletons in High-Current Laboratory Discharges. Extrapolation to Ball Lightning. Abstracts of the 2001 International Symposium on Ball Lightning (and references cited therein).

17. Kukushkin, A.B. and Rantsev-Kartinov, V.A. (2004) A Hybrid of Aerogel and Plasma Models of Ball Lightning: An Inductive Storage Wildly Formed by a Nanotube-Assembled Skeleton. 31st EPS Conference on Plasma Phys. London, ECA Vol. 28G, P-4.089.

18. Abrahamson, J. and Dinniss, J. (2000) Ball lightning caused by oxidation of nanoparticle networks from normal lightning strikes on soil. Nature 403, 519–521.

19. Abrahamson, J. and Marshall, J. (2002) Permanent electric dipoles on gas-suspended particles and the production of filamentary aggregates. J. Electrostat. 55, 43–63.

20. Abrahamson, J. (2002) Ball lightning from atmospheric discharges via metal nanosphere oxidation: from soils, wood or metals. Philos. Trans. R. Soc. Lond. A 360, 61–88.

21. Bychkov, V.L., Bychkov, A.V., and Stadnik, S.A. (1996) Polymer balls in discharge plasma. Phys. Scr. 53, 749–759.

22. Bychkov, V.L. (2002) Polymer-composite ball lightning. Philos. Trans. R. Soc. Lond. A 360, 37–60 and references therein.

23. Kikuchi, H. (1996) Roles of dust or object perturbing an electric cusp in electric reconnection and consequent electric discharge or lightning. Phys. Chem. Earth 21, 549.

24. Turner, D.J. (2002) The fragmented science of ball lightning (with comment). Philos. Trans. R. Soc. Lond. A 360, 107–152.

25. Sanduloviciu, M. and Lozneanu, E. (2000) Ball lightning as a self-organization phenomenon. J. Geophys. Res. 105, 4719.

26. Ohtsuki, Y. and Ofuruton, H. (1991) Plasma fireballs formed by microwave interference in air. Nature 350, 139.

27. Brandenburg, J.E. and Kline, J.F (1998) Experimental investigation of large-volume PIA plasmas at atmospheric pressure. IEEE Trans. Plasma Sci. 26, 145.

28. Tanaka, K. and Tanaka, M. (1997) Is ball lightning “Anderson Localization”? Appl. Phys. Lett. 71, 3793.

29. Chandrasekhar, S. and Fermi, E. (1953) Problems of gravitational stability in the presence of a magnetic field. Ap. J. 118, 116.

30. Shafranov, V.D. (1966) Reviews of Plasma Physics. Vol. 2. M.A. Leontovich, Consultants Bureau, New York.

31. Marsh, G. (1996) Force-Free Magnetic Fields: Solutions, Topology and Applications. World Scientific, Singapore.

32. Wua, H. and Oakes, M.E. (1991) Magnetohydrodynamics equilibrium of a self-confined elliptical plasma ball. Phys. Fluids B 3, 2113.

33. Faddeev, L. and Niemi, A.J. (2000) Magnetic geometry and the confinement of electrically conducting plasmas. Phys. Rev. Lett. 85, 3416.

34. Faddeev, L., Freyhult, L., Niemi, A.J., and Rajan, P. (2002) Shafranov’s virial theorem and magnetic plasma confinement. J. Phys. A Math. Gen. 35, 133.

35. Bergström, A. (1973) Electromagnetic theory of strong interaction. Phys. Rev. D 8, 4394.

36. Shmatov, M.L. (2003) New model and estimation of the danger of ball lightning. J. Plasma Phys. 69, 507.

37. Rañada, A.F. and Trueba, J.L. (1996) Ball lightning an electromagnetic knot? Nature 383, 32.

38. Rañada, A.F., Soler, M., and Trueba, J.L. (1998) A model of ball lightning as a magnetic knot with linked streamers. J. Geophys. Res. 103, 23309–23313.

39. Kaiser, R. and Lortz, D. (1995) Ball lightning as an example of magnetohydrodynamic equilibrium. Phys. Rev. E 52, 3034–3044.

40. Bogoyavlenskij, O.I. (2002) Symmetry transforms for ideal magnetohydrodynamics equilibria. Phys. Rev. E 66, 056410.

41. Lowke, J.J. (1996) A theory of ball lightning as an electric discharge. J. Phys. D Appl. Phys. 29, 1237–1244.

42. Lowke, J.J. (2004) On the physics of lightning. IEEE Trans. Plasma Sci. 32, 4–17.

43. Endean,V.G. (1993) Spinning electric dipole model of ball lightning. IEEE Proc. A 140, 474–478.

44. Mesenyashin, A.I. (1991) Electrostatic and bubble nature of ball lightning. Appl. Phys. Lett. 58, 2713–2715.

45. Mesenyashin, A.I. (1995) Spherical formations in the atmosphere as a physical phenomenon. J. Electrostat. 36, 139–150.

46. Natyaganov, V.L. (2003) An electro capillary eddy model of ball lightning. Dokl. Phys. 48, 319–322.

47. Nikitin, A.I. (1999) The Dynamic Capacitor Model of Ball Lightning. Proc. of 6th International Symposium on Ball Lightning (ISBL99). Antwerp, Belgium. pp. 91–95.

48. Torchigin, V.P. (2003) On the nature of ball lightning. Dokl. Phys. 48, 108–111.

49. Torchigin, V.P. and Torchigin, A.V. (2004) Behavior of self-confined spherical layer of light radiation in the air atmosphere Phys. Lett. A 328, 189–195.

50. Torchigin, V.P. and Torchigin, A.V. (2005) Features of ball lightning stability. Eur. Phys. J. D 32, 383–389.

51. Fredkin, D.R. and Mayergoyz, I.D. (2003) Resonant behavior of dielectric objects (electrostatic resonances). Phys. Rev. Lett. 91, 253902.

52. Mayergoyz, I.D., Fredkin, D.R., and Zhang, Z. (2005) Electrostatic (plasmon) resonances in nanoparticles. Phys. Rev. B 72, 155412.

53. Gillman, J.J. (2003) Cohesion in ball lightning. Appl. Phys. Lett. 83, 2283–2284.

54. Conde, L. and León, L. (1994) Multiple double layer in a glow dischargue. Phys. Plasmas 1, 1171.

55. Pohoata, V., Popa, G., Schittwieser, R., Ionita, C., and Cercek, M. (2003) Properties and control of an anode double layer oscillations and related phenomena. Phys. Rev. E 68, 016405.

56. Alexeff, I., Parameswaran, S., Thiayagrajan, M., and Grace, M. (2005) An observation of synthetic ball lightning. IEEE Trans. Plasma Sci. 33(2), 498–499.

57. Alexeff., I. and Rader, M. (1992) Observation of closed loops in high-voltage discharges: a possible precursor of magnetic flux trapping. IEEE Trans. Plasma Sci. 20(6), 669–671.

58. Alexeff, I. and Rader, M. (1995) Possible precursors of ball lightning – observation of closed loops in high-voltage discharges. Fusion Technol. 27, 271.

59. Koloc, P. ISBL89 and comments of Reece Roth, J. (1997) Ball lightning: what nature is trying to tell fusion community. In Current Trends in International Fusion Research. Panarella, E., Ed. Plenum Press, New York.

60. Chen, C., Pakter, R., and Seward, D.C. (2001) Equilibrium and stability properties of self-organized electron spiral toroids. Phys. Plasmas 8, 4441–4449.

61. Avramenko, R.F., Nikolaeva, V.I., and Poskacheeva, L.P. (1994) Ball Lightning in Laboratory: A Collection of Articles. Khimiya, Moscow.

62. Dijkhuis, G.C., Ed. (1999) Proceedings of the 6th International Symposium on Ball Lightning (ISBL99). Antwerp, Belgium.

63. Shavanov, G.D. (2002) The optical properties of long-lived luminous formations. Tech. Phys. Lett. 28, 164–166

64. Emelin, S.E., Semenov, V.S., Bychkov, V.L., Belisheva, N.K., and Kovshik, A.P. (1997) Some objects formed in the interaction of electrical discharges with metals and polymers. Tech. Phys. 42, 269–277.

65. Emelin, S.E., Pirozerski, A.L., Skvortsov, G.E., and Bychkov, V.L. (2002) Long-living plasma formations arising from metal wires burning, Preprint http://xxx.lanl.gov/html/physics/0208062; See also http://balllightning.narod.ru for more images.

66. Egorov, A.I. and Stepanov, S.I. (2002) Long-lived plasmoids produced in humid air as analogues of ball lightning. Tech. Phys. 47, 1584–1586.

67. Tsytovich, V.N. (1998) One-dimensional self-organised structures in dusty plasmas. Aust. J. Phys. 51, 763–834.

68. Smirnov, B.M. (1993) Physics of ball lightning. Phys. Rep. 224, 151.

69. Tsui, K.H. (2001) Force-free field model of ball lightning. Phys. Plasmas 8, 687–689.

70. Tsui, K.H. (2003) Ball lightning as a magnetostatic spherical force-free plasmoid. Phys. Plasmas 10, 4112–4117.

71. Moffatt, H.K. (1969) The degree of knottedness of tangled vortex lines. J. Fluid Mech. 35, 117.

72. Moffatt, H.K. (2000) Vortex and magneto-dynamics. A topological perspective. In Mathematical Physics. Imperial College, London.

73. Rañada, A.F. (1992) On the magnetic helicity. Eur. J. Phys. 13, 7076.

74. Trueba, J.L. and Rañada, A.F. (1996) The electromagnetic helicity. Eur. J. Phys. 17, 141.

75. Callebaut, D.K. (2004) Energy Storage by Force-Free Magnetic Fields in the Initial Phase of Ball Lightning. 8^th International Symposium on Ball Lightning (ISBL04).

76. Trubnikov, B.A. (2002) Current filaments in plasmas. Plasma Phys. Rep. 28, 312–326.

77. Vlasov, V.P. and Trubnikov, B.A. (2003) Quasi-stability of a plasma bicylinder. Tech. Phys. 48, 858–865.

78. Oliveira, S.R. and Tajima, T. (1995) Generalized relaxation theory and vortices in plasma. Phys. Rev. E 52, 4287–4293.

79. Chandrasekhar, S. and Woltjer, L. (1958) On force-free magnetic fields. Proc. Natl. Acad. Sci. U. S. A. 44, 285.

80. Gekelman, W., Maggs, J.E., and Pfister, H. (1992) Experiments on the interaction of current channels in a laboratory plasma: relaxation to force-free state. IEEE Trans. Plasma Sci. 20, 614–621.

81. Rañada, A.F., Soler, M., and Trueba, J.L. (2000) Ball lightning as a force-free magnetic knot. Phys. Rev. 62, 7181–7190.

82. Rañada, A.F. (1992) Topological electromagnetism. J. Phys. A Math Gen. 25, 1621–1641.

83. Rañada, A.F. and Trueba, J.L. (1995) Electromagnetic knots. Phys. Lett. A 202, 337.

84. Taylor, J.B. (1974) Relaxation of toroidal plasma and generation of reverse magnetic fields. Phys. Rev. Lett. 33, 1139.

85. Taylor, J.B. (1986) Relaxation and magnetic reconnection in plasmas. Rev. Mod. Phys. 58, 741.

86. Yoshida, Z., Ohsaki, S., Ito, A., and Mahajan, S.M. (2003) Stability of Beltrami flows. J. Math. Phys. 44, 2168.

87. Cheviakov, A.F. (2005) Analytical 3-dimensional plasma equilibria. Topol. Appl. 152, 157–173.

88. Cheviakov, A.F. (2005) Construction of exact plasma equilibrium solutions with different geometries. Phys. Rev. Lett. 94, 16.

89. Rañada, A.F., Trueba, J.L., and Donoso, J.M. (2005) Ball lightning. In Encyclopedia of Nonlinear Science. Scott, A., Ed. Fitzroy Dearborn, London. p. 39.

90. Donoso, J.M., Salgado, J.J., and Soler, M. (2005) Non-linear Fokker–Planck integral propagator for plasma kinetic coefficients. J. Phys. A Math. Gen. 38, 9145–9158.

91. Arrayás, M., Ebert, U., and Hundsdorfer, W. (2002) Spontaneous branching of anode-directed streamers between planar electrodes. Phys. Rev. Lett. 88, 174502.

92. Liu, N. and Pasko, V.P. (2004) Effects of photoionization on propagation and branching of positive and negative streamers in sprites. J. Geophys. Res. 109, 1–17.

93. Arrayás, M., Fontelos, M.A., and Trueba, J.L. (2005) On the mechanism of branching in negative ionization fronts. Phys. Rev. Lett. 95, 165001.

Este artículo debe citarse como sigue:

Donoso, J.M., Trueba, J.L., y Rañada, A.F. (2006) The riddle of ball lightning: a review. The Scientific World Journal 6, 254-278. DOI 10.1100/tsw.2006.48.

BIOGRAFÍAS

José M. Donoso es profesor del Departamento de Física Aplicada de la Universidad Politécnica (ETSI Aeronáuticos) de Madrid, España. Obtuvo su doctorado en la Universidad Complutense de Madrid sobre métodos integrales numéricos para la ecuación de Física de Plasmas de Fokker-Planck. En la actualidad, estudia los efectos cinéticos no lineales en los procesos de transporte de plasma en los que intervienen campos electromagnéticos y el cálculo numérico de ecuaciones de plasma no lineales.

José L. Trueba es profesor en el Departamento de Física Aplicada de la Universidad Rey Juan Carlos, Móstoles, España. Estudió Física en la Universidad Autónoma de Madrid y se doctoró en la Universidad Complutense de Madrid sobre configuraciones topológicas en electromagnetismo clásico, incluyendo un modelo de centella. Sus principales intereses son los nudos electromagnéticos, la física de plasmas y las ondas en medios excitables.

Antonio Fernández-Rañada es Catedrático de Física en la Universidad Complutense de Madrid, España, desde 1976. Tras trabajar varios años en física de partículas elementales después de doctorarse en la Universidad de París, sus intereses profesionales han sido la física cuántica y la dinámica no lineal, y después los campos topológicos, proponiendo un modelo de electromagnetismo en el que algunas magnitudes como la carga y la energía en una cavidad obedecen a reglas de cuantización debidas a la configuración topológica de las líneas de campo. Esto inspiró un modelo de centella, en el que el enlace de las líneas magnéticas aumenta la estabilidad de las bolas de fuego. Actualmente trabaja en cosmología, donde propuso un modelo para la anomalía Pioneer. Fundó y dirigió durante 10 años la Revista Española de Física y fue miembro del Consejo de Ética de la Investigación Científica y Técnica de la Fundación Española para la Ciencia. Actualmente es presidente de la Real Sociedad Española de Física.