Muchas felicidades a quienes coincidimos en cumpleaños en este día: Alejandro Agostinelli, Vidal Belduque, Michelle Pfiffer, Uma Thurman, el tal Noguez…, pero sobre todo a Marcianitos Verdes que cumple 18 años.
Muchas felicidades a quienes coincidimos en cumpleaños en este día: Alejandro Agostinelli, Vidal Belduque, Michelle Pfiffer, Uma Thurman, el tal Noguez…, pero sobre todo a Marcianitos Verdes que cumple 18 años.
Archivo de la categoría: Divulgación científica
El factor olvidado: El efecto psicológico de los FANI
El factor olvidado: El efecto psicológico de los FANI
El profesor Gabriel de la Torre llama la atención sobre la necesidad de estudiar los FANIU no sólo desde el punto de vista físico y tecnológico, sino también a través de los efectos psicológicos en los testigos.
5 de abril de 2024
Por Dr. Gabriel de la Torre
Actualmente estamos viviendo una época turbulenta de Fenómenos Anómalos No Identificados o también conocidos como FANI. Por un lado, tenemos a los cada vez más numerosos grupos, fundaciones y asociaciones de científicos que abogan por una desclasificación y estudio científico de este fenómeno, y por otro, a las autoridades que, divididas, tratan de restar importancia al asunto. Ejemplo de ello son las últimas declaraciones ante el Congreso de los Estados Unidos, los informes de la NASA, el Pentágono y las diferentes respuestas en prensa y redes sociales.
Todo ello tiene un denominador común, el foco de atención está en los objetos. Los objetos son de enorme interés, tanto para los de un lado como para los del otro. Sin duda, entender estos fenómenos que parecen desafiar nuestra física es un gran reto y tiene un interés que va más allá de la mera curiosidad ya que pueden representar el mayor enigma de nuestra Historia. A qué potencia mundial no le interesaría entender cómo algo, un objeto, una tecnología puede superar los límites actuales asumidos de velocidad, aceleración, invisibilidad, etc. Podría ser una ventaja decisiva en el ámbito estratégico. Por tanto, los FANI pueden representar una amenaza para la seguridad nacional, como se ha dicho en distintos foros, pero también una oportunidad, una oportunidad de avance tecnológico, una singularidad tecnológica.
Interés por eliminar el estigma de los avistamientos de FANI
Por otro lado, tenemos un fenómeno que durante años ha sido menospreciado, ridiculizado y olvidado por la comunidad científica. Para la Ciencia estas cosas que se veían en el cielo probablemente tenían una explicación razonable, pájaros, globos, estrellas, etc. Sin embargo, recientemente han aparecido en escena nuevos objetos que han añadido confusión y preocupación: los drones, o vehículos aéreos no tripulados (UAV). Estos drones pueden variar mucho en tamaño y características y tienen una cualidad que los hace preocupantes: pueden ser difíciles de detectar y a veces pueden confundirse con los FANI. ¿Qué pasaría entonces si los pilotos, militares y civiles fueran testigos de UAV que sobrevuelan áreas de interés estratégico o zonas de exclusión aérea, y no los denunciaran por miedo al ridículo al parecerse a los FANI? Esto había que cambiarlo, había que eliminar el estigma no sólo en la ciencia sino en la sociedad. Debemos ser conscientes de que el enemigo puede utilizar esta tecnología UAV sobre territorio nacional y pasar prácticamente desapercibido (por ejemplo, los recientes supuestos globos chinos). Ahora debemos mirar al cielo y analizar, informar y estudiar objetos sobre los que antes guardábamos silencio por miedo a las consecuencias.
Por lo tanto, debemos partir de un nuevo paradigma de concienciación sobre las amenazas en nuevos ámbitos y el anterior estigma de “útil” de los FANI ha perdido su utilidad una vez que los vehículos aéreos no tripulados han entrado en escena. Si a esto añadimos el potencial diferenciador de los datos obtenidos del estudio de los FANI para el desarrollo tecnológico, el cambio de paradigma parecía inevitable, aunque lógicamente con reservas.
La información sigue fluyendo a cuentagotas, incompleta y con gran dificultad, a veces en bucle. Hace años existieron varios programas de estudio sobre los antes llamados ovnis (objetos voladores no identificados). Como sabrán, todos ellos fueron infructuosos, pero algunos arrojaron datos interesantes. El Dr. Allen Hynek fue uno de estos primeros científicos que estudió este tema primero desde el lado escéptico/gobierno y luego desde el otro lado.
El factor tecnológico oculta el factor humano
Cabe preguntarse cuál es el factor hegemónico en el estudio e interés actual por los FANI, tanto por parte de la comunidad científica (grupos, asociaciones, fundaciones, etc.) como por parte de las autoridades en sus diferentes niveles. En mi opinión es claramente el tecnológico.
En este enfoque materialista se olvida, desde mi punto de vista, el factor fundamental, el factor humano. Los FANI suelen estar vinculados a una persona, aunque sea una persona que interpreta los datos de un sensor en un radar, un humano que pilota un avión, etc. o un grupo de humanos que interactúa en un momento dado con uno o varios FANI. En algunos casos, estos testigos incluso interactúan con los ocupantes de FANI. Este factor humano ha sido utilizado por el escepticismo, para desacreditar a los testigos o para explicar los avistamientos. Curiosamente, estos argumentos rara vez han sido contrastados por expertos en Psicología, Neurociencia o similares, salvo excepciones.
Actualmente es como si se estuviera produciendo una revisión del fenómeno, más comités, sesiones informativas, etc. Echo de menos referencias a aquellos científicos que en su día estudiaron los aspectos psicológicos y sociológicos de los encuentros FANI, no sin dificultad como el Dr. Ring, el Dr. Mack, sin embargo comúnmente vemos referencias al Dr. Valle, astrónomo.
En mi opinión el factor psicológico es clave para entender los FANI. Por supuesto, es bueno entender su física, pero si se trata de objetos inteligentes, ¿cuál es su propósito? ¿Qué efectos tienen sobre los observadores? A primera vista, algunos pueden pensar que ninguno. Sin embargo, hay ejemplos de algunos casos en los que se han producido efectos físicos en los testigos, pero también hay un efecto que a menudo se ha ignorado, el efecto psicológico.
Nuestro estudio sobre los aspectos psicológicos relacionados con las FANI
En nuestro estudio (“Psychological aspects in unidentified anomalous phenomena (UAP) witnesses”), publicado recientemente en la revista científica International Journal of Astrobiology (DOI: 10.1017/S1473550423000289) nos centramos precisamente en el análisis de estas variables psicológicas en testigos de FANI. El estudio consistió en un cuestionario, mayoritariamente tipo Likert, dividido en 5 secciones fundamentales.
§ En primer lugar, recogimos información básica sobre los participantes (245 voluntarios de distintos países), como nivel educativo, edad, etc.
§ En una segunda sección hicimos varias preguntas sobre los videos populares sobre FANI y la US Navy que se publicaron en prensa con gran repercusión social. También se incluyeron aquí varias preguntas sobre la posición respecto a los FANI de los gobiernos y de la ciencia sobre este tema.
§ En una tercera sección formulamos preguntas sobre el tema de la búsqueda de inteligencia extraterrestre. Muchas de estas preguntas estaban relacionadas con las diferentes estrategias, hipótesis y teorías utilizadas por los científicos en este ámbito.
§ Una cuarta sección estaba dedicada a los propios FANI, sus características, origen, etc.
§ La última sección, la quinta, era una sección a la que sólo podían acceder aquellos participantes que declararon haber sido testigos directos de un avistamiento o experiencia con FANI (93 sujetos). En esta última sección, las preguntas estaban relacionadas con el incidente, e hicimos hincapié en la recogida de datos e información sobre las posibles consecuencias psicológicas, fisiológicas o físicas y las pruebas que pudieran tener.
Los resultados de nuestro estudio arrojaron algunos datos interesantes. Parece que los FANI tienen un efecto común en muchos testigos, básicamente se podría decir que se introducen, digamos, en la mente de los testigos, y generalmente el tema de los FANI ocupará un lugar relevante en su pensamiento.
La tríada del compromiso profundo con los FANI
Identificamos lo que hemos denominado la tríada del compromiso psicológico profundo con los FANI, que consta de tres factores fundamentales:
1. los testigos se sienten algo obsesionados con el fenómeno (no patológico),
2. necesitan hablar de ello, aunque no se trate de su propia experiencia o suceso.
3. y el tema FANI está presente en sus pensamientos en algún momento del día, todos los días.
Los FANI tienen un efecto transformador en las personas que los presencian y en sus sistemas de creencias respecto a aspectos concretos como la vida en el universo. Se produce una especie de cambio de conciencia. Si tenemos en cuenta que se producen cientos, quizá miles, de avistamientos al año, podría decirse que el efecto es global, ¿quizá intencionadamente global?
Nuestros participantes informaron en menor medida de efectos fisiológicos y, en algunos casos, perceptivos, incluso días después del suceso o avistamiento.
El perfil psicológico de los testigos de FANI
También es interesante el perfil psicológico de estos testigos con detalles característicos como la no relevancia del componente religioso, la resiliencia ante sucesos traumáticos y la vida espiritual entre otros.
La información aportada por los testigos es muy relevante para la comprensión del fenómeno en nuestra opinión y mientras nos dedicamos a tratar de entender ciertas características físicas que van más allá de nuestra comprensión actual, estamos perdiendo una valiosa fuente de información que, si bien ha sido durante años atendida en la investigación del fenómeno, no lo era desde el ámbito académico o científico en la misma medida.
Por ello, entiendo que, ante un fenómeno incomprensible para nosotros, no necesariamente aéreo, como son los FANI, la búsqueda de patrones y datos más interesantes puede estar donde menos hemos mirado, en los testigos. Imaginemos que un día vamos a Marte y encontramos una instalación nuclear y un marciano, ¿qué sería más interesante estudiar, al marciano o su tecnología nuclear?
Ya he escrito anteriormente sobre la facilidad con la que nuestra atención y percepción se desvían debido a las limitaciones de nuestra propia mente, nuestro cerebro. Se propuso el llamado efecto gorila cósmico (De la Torre, G.G. & García, M. A. (2018). El efecto gorila cósmico o el problema de las señales inteligentes no terrestres no detectadas. Acta Astronáutica, 146, 83-91.), basado en estudios clásicos en Psicología (Ceguera Inatenta/Gorila Invisible de Chabris y Simons en los años 90 y 2010). Este efecto gorila cósmico explica cómo aunque tuviéramos un extraterrestre delante de nuestras narices, no lo veríamos. Este efecto gorila cósmico explica cómo, aunque tuviéramos un extraterrestre delante de nuestras narices, no lo veríamos. Nos distraemos con otros detalles mientras los importantes pasan desapercibidos, no seríamos conscientes de ello. La atención está relacionada con la percepción y la acción, pero aún más importante con la Consciencia.
https://uapdigital.com/noticias/the-forgotten-factor-the-psychological-effect-of-the-uap/
Aspectos psicológicos en testigos de fenómenos anómalos no identificados (FANI)
Publicado en línea por Cambridge University Press: 11 de diciembre de 2023
Gabriel G. De la Torre[Abre en ventana nueva]
Resumen
En este estudio, encuestamos a un total de 245 personas sobre fenómenos anómalos no identificados (FANI), 93 de las cuales fueron testigos directos de FANI. Prestando especial atención al impacto psicológico de los FANI, la encuesta de nuestro estudio abarcó diferentes aspectos, como las opiniones sobre los comunicados oficiales sobre los FANI, el enfoque científico de los fenómenos y la búsqueda de inteligencia extraterrestre. Este estudio descubrió que los FANI tenía un claro impacto psicológico en los testigos, con un efecto transformador, y una forma benigna de interés no patológico de tipo obsesivo por el tema que definimos como la tríada del compromiso psicológico profundo de los FANI. Esta tríada de compromiso psicológico profundo se caracteriza porque el tema FANI está presente en la mente del testigo a diario, con un interés y aprecio por el tema reconocidos por él mismo y una necesidad de hablar sobre el tema FANI, no necesariamente sobre el suceso que experimentó. Los FANI parecen tener un impacto muy específico centrado en los aspectos extraterrestres y en el propio fenómeno, que los testigos directos experimentan como un acontecimiento que les cambia la vida. Estos aspectos psicológicos son cuantitativa y cualitativamente objetivables, y es necesario seguir investigando en esta dirección, ya que todos los esfuerzos de investigación parecen centrarse actualmente en los aspectos físicos de estos fenómenos.
Palabras clave
cogniciónpsicologíaextraterrestreUAP
Tipo
Artículo de investigación
Información
Revista Internacional de Astrobiología , Volumen 23 , 2024 , e4
DOI: https://doi.org/10.1017/S1473550423000289[Abre en ventana nueva]
Este es un artículo de acceso abierto, distribuido bajo los términos de la licencia Creative Commons Attribution (http://creativecommons.org/licenses/by/4.0/), que permite su reutilización, distribución y reproducción sin restricciones, siempre que se cite adecuadamente el artículo original.
Derechos de autor
Copyright © Los autores, 2023. Publicado por Cambridge University Press
Introducción
A pesar de los esfuerzos pasados y presentes por explicar la naturaleza de los fenómenos aéreos no identificados o fenómenos anómalos no identificados (FANI), también conocidos como objetos voladores no identificados (ovni), no hemos tenido un éxito notable. Tal vez esto se deba a que la comunidad científica ha rechazado con algunas excepciones concretas, por ejemplo el Proyecto Hessdalen en Noruega (Teodorani, Referencia Teodorani2004) el estudio de estos fenómenos durante muchos años, y sólo más recientemente científicos de diferentes disciplinas han comenzado a realizar más investigaciones científicas sobre este tema. Sin embargo, las agencias gubernamentales han mostrado mayor interés en los FANI durante décadas, iniciando programas de investigación oficiales y secretos, incluyendo el Proyecto Sign(1949), el Proyecto Grudge – Oficina de Desclasificación de la Fuerza Aérea(1949), Objetos Voladores No Identificados y el Proyecto Libro Azul de la Fuerza Aérea(1952-1969) y el Programa de Aplicación Especial de Armas Aeroespaciales Avanzadas (AAWSAP; 2007), incluso a veces financiando esfuerzos adicionales de investigación privada en esta dirección. Actualmente, la mayoría de los esfuerzos de la comunidad científica se centran en los aspectos físicos de los FANI, como la aceleración, la velocidad, la maniobrabilidad, etc. Varias iniciativas privadas han puesto en marcha procedimientos y programas de observación y análisis sistemáticos para tratar de identificar las características físicas exactas de los FANI. La Coalición Científica para el Estudio de los FANI (SCU; https://www.explorescu.org/) se ha esforzado notablemente en el análisis de los resultados de los supuestos videos de infrarrojos de puntería avanzada (Advanced Targeting Forward Looking Infrared, ATFLIR) de los FANI durante los encuentros del Nimitz en 2004 (Knuth et al., Referencia Knuth, Powell y Reali2019), popularizados por primera vez por The New York Times (Cooper et al., Referencia Cooper, Blumenthal y Kean2017). El Proyecto Galileo es otra iniciativa reciente del profesor de Ciencias Avi Loeb (Universidad de Harvard), destinada al estudio científico de las firmas tecnológicas extraterrestres, incluidos los FANI, utilizando un método extensivo de detectores de señales bajo el enfoque de interpretación del modelo de física estándar (Loeb, Referencia Loeb2022). El Proyecto Galileo parece un esfuerzo complementario a la tradicional Búsqueda de Inteligencia extraterrestre (SETI).
Si los estudios científicos sobre el fenómeno no son numerosos y son relativamente recientes y serios cuando se trata de comprender la física y la aerodinámica del FANI, la investigación psicológica sobre el FANI es aún más escasa. En cuanto a los aspectos psicológicos, se han realizado algunas investigaciones en el pasado, en su mayoría estudios vagos que intentan explicar los relatos de los observadores, o historias que aluden a cuestiones relacionadas con la psicología, como la parálisis del sueño, la histeria colectiva, las alucinaciones, etc. (Olmos, Referencia Olmos1994; Swami et al., Referencia Swami, Pietschnig, Stieger y Voracek2010; Dagnall et al., Referencia Dagnall, Drinkwater y Parker2011; Escolà-Gascón, Referencia Escolà-Gascón2020; Yingling et al., Referencia Yingling, Yingling y Bell2023). Existen algunas investigaciones sobre aspectos psicológicos y testigos que informaron de encuentros cerrados con ovnis o sus supuestos ocupantes (Jung, Referencia Jung1959; Ring, Referencia Ring1993; Mack, Referencia Mack2000).
Los fenómenos FANI representan un desafío, no sólo para la ciencia, sino también para nuestras propias percepciones, razonamientos y psiques; no encajan en nuestro sistema de creencias, normas o expectativas. La naturaleza innovadora de los FANI es muy interesante, sobre todo en el ámbito psicológico. En muchos casos, los testigos quedan en estado de shock e incredulidad, con sentimientos perturbadores, y esto puede tener un efecto que cambie la vida de algunos. En el presente estudio, nuestro objetivo fue indagar en estos efectos psicológicos de los FANI, analizar y comparar los resultados obtenidos mediante una encuesta de escala Likert con preguntas relacionadas con los FANI y la búsqueda de inteligencia extraterrestre (IE) en general.
Métodos
Una muestra de 245 participantes (68.15% hombres, 18.15% mujeres) participó en una encuesta de forma voluntaria y anónima. De la muestra, el 37.10% había completado o declaraba haber completado algún nivel de estudios universitarios, mientras que el 15.73% declaraba haber finalizado estudios universitarios, y el 25.41% tenía un nivel de estudios de postgrado. La encuesta estaba disponible, en inglés, distribuida en línea y accesible a personas interesadas en los temas de FANI y SETI de todo el mundo.
La encuesta constaba de 72 preguntas, divididas en cuatro secciones. La primera sección contenía preguntas relativas a los videos publicitados sobre FANI por el Pentágono estadounidense, incluidos los encuentros del Nimitz. Estas preguntas pretendían tanto evaluar si los participantes conocían estos videos como recabar su opinión sobre ellos y sus posibles implicaciones para futuras investigaciones. La segunda sección de la encuesta contenía preguntas relacionadas con las opiniones de los participantes acerca de la investigación científica sobre la búsqueda del EI, en general. Aquí las preguntas se referían a los mejores instrumentos o enfoques para realizar esta búsqueda, los resultados de la búsqueda, las implicaciones sociales y la implicación de los encuestados en estas actividades o comunidades científicas. La tercera sección evaluaba información demográfica general y aspectos psicológicos, incluyendo habilidades y estilos cognitivos, rasgos generales de personalidad, creencias religiosas, espiritualidad, etc. Por último, una cuarta sección estaba dedicada a los testigos de un incidente de violencia de género, y sólo estaba disponible para los encuestados que también confirmaron ser testigos directos de un incidente de violencia de género. En esta sección, recogimos información sobre el incidente y las consecuencias posteriores al mismo, tanto en el ámbito fisiológico como en el psicológico. Noventa y tres (37.5%) de los participantes declararon haber sido testigos directos de un incidente de abuso sexual. La mayoría de las preguntas presentaban una forma de escala de Likert, en la que los participantes debían responder utilizando una escala del 1 al 5 de “totalmente en desacuerdo” con la pregunta o afirmación, o “totalmente de acuerdo” con ella. Menos frecuentes eran las preguntas que pedían respuestas de “sí/no”, de texto corto o de opción múltiple.
Aunque en este estudio nos hemos centrado principalmente en los aspectos psicológicos, merece la pena destacar algunas respuestas de otras secciones de nuestra encuesta. Por ejemplo, el 45.56% de los participantes afirmaron no saber qué podían ser los FANI en los videos del Pentágono. Aunque los participantes reconocieron que no podían identificar o explicar qué podían ser estos FANI, estuvieron mayoritariamente de acuerdo en que los FANI mostraban características no convencionales en cuanto a velocidad, maniobrabilidad y capacidades, y también consideraron que la comunidad científica y los gobiernos deberían llevar a cabo más investigaciones sobre los FANI para intentar aclarar su origen (91.90%). En general, se midieron los aspectos psicológicos de los participantes con varias preguntas que abarcaban los estilos cognitivos (principalmente intuitivo frente a racional), las capacidades de atención y memoria, la calidad del sueño, la percepción, los rasgos de personalidad y los pensamientos.
Resultados
El efecto psicológico de los FANI en los testigos y también en las personas interesadas fue claramente transformador, según los resultados de nuestra encuesta. También es interesante observar algunos perfiles específicos de los testigos y algunos aspectos psicológicos, como una clara tendencia de comportamiento/pensamiento de compromiso hacia el tema. A continuación analizaremos con más detalle estos resultados.
En general, entre los participantes en la encuesta había testigos directos y no testigos. Las características de la muestra global que respondió a nuestras preguntas psicológicas generales son muy estándar, con sólo un par de particularidades dignas de mención, como que la mayoría de ellos se describieron a sí mismos como espirituales, pero no religiosos (Mdn 3, Mode 5, DE 1.44). Asimismo, las personas informaron de un perfil cognitivo mayoritariamente intuitivo (Mdn 4, Modo 4, DE 0.82), frente a racional. Los participantes declararon no tener problemas de sueño, no predominar la introversión frente a la extroversión y tener una buena capacidad de atención, en general (Tabla 1). Sin embargo, el 45.5% de los participantes declararon haber sido víctimas de acoso escolar en el pasado y/o haber sufrido traumas psicológicos y un porcentaje similar mostró que miembros de su familia también estaban interesados en el tema.
Tabla 1. Resultados descriptivos de las preguntas sobre aspectos psicológicos generales (muestra global)
 En la muestra general/global, para las preguntas relacionadas con los FANI en general, algunos resultados apoyaron claramente argumentos como que los gobiernos (Mdn 5, Modo 5, DE 0.76) y los científicos (Mdn 5, Modo 5, DE 0.70) deberían prestar más atención a los fenómenos y estudiarlos; asimismo, los encuestados pensaban que estamos siendo visitados por inteligencia no terrestre (Mdn 4, Modo 5, DE 1,14). Sin embargo, hubo división de opiniones en cuanto al origen extraterrestre de los FANI y los posibles resultados o riesgos de los contactos con la IE (Tabla 2).
En la muestra general/global, para las preguntas relacionadas con los FANI en general, algunos resultados apoyaron claramente argumentos como que los gobiernos (Mdn 5, Modo 5, DE 0.76) y los científicos (Mdn 5, Modo 5, DE 0.70) deberían prestar más atención a los fenómenos y estudiarlos; asimismo, los encuestados pensaban que estamos siendo visitados por inteligencia no terrestre (Mdn 4, Modo 5, DE 1,14). Sin embargo, hubo división de opiniones en cuanto al origen extraterrestre de los FANI y los posibles resultados o riesgos de los contactos con la IE (Tabla 2).
Tabla 2. Resultados de las preguntas generales sobre FANI (muestra global)
 Noventa y tres participantes declararon ser testigos directos de FANI, y fueron redirigidos a una sección especial con preguntas sólo disponibles para testigos de FANI. El objetivo de estas preguntas era recabar información sobre los posibles efectos, consecuencias y características de la violencia de género. Fue muy interesante observar algunas pautas en las respuestas de los participantes en esta sección. El aspecto más relevante fue lo que hemos identificado como el UAP-DPET, en el que tres condiciones muy interrelacionadas y estadísticamente correlacionadas, como confirmó la prueba de correlación de Spearman, parecían características de los testigos de FANI. Estas tres condiciones o aspectos se refieren a una forma particular de compromiso psicológico profundo o rasgo psicológico, que incluye que el tema de los FANI esté presente casi todos los días en sus mentes; reconocen estar muy interesados o a veces obsesionados con el tema; y sienten la necesidad de hablar de ello (Tablas 3 y 4).
Noventa y tres participantes declararon ser testigos directos de FANI, y fueron redirigidos a una sección especial con preguntas sólo disponibles para testigos de FANI. El objetivo de estas preguntas era recabar información sobre los posibles efectos, consecuencias y características de la violencia de género. Fue muy interesante observar algunas pautas en las respuestas de los participantes en esta sección. El aspecto más relevante fue lo que hemos identificado como el UAP-DPET, en el que tres condiciones muy interrelacionadas y estadísticamente correlacionadas, como confirmó la prueba de correlación de Spearman, parecían características de los testigos de FANI. Estas tres condiciones o aspectos se refieren a una forma particular de compromiso psicológico profundo o rasgo psicológico, que incluye que el tema de los FANI esté presente casi todos los días en sus mentes; reconocen estar muy interesados o a veces obsesionados con el tema; y sienten la necesidad de hablar de ello (Tablas 3 y 4).
Tabla 3. Datos descriptivos del UAP-DPET (muestra testigo; n = 80)
 Tabla 4. Matriz de correlación del UAP-DPET y los componentes de espiritualidad/religión (muestra de testigos, n = 80)
Tabla 4. Matriz de correlación del UAP-DPET y los componentes de espiritualidad/religión (muestra de testigos, n = 80)
 Nota. *p < 0.05, **p < 0.01, ***p < 0.001.
Nota. *p < 0.05, **p < 0.01, ***p < 0.001.
Los resultados obtenidos de la muestra de testigos no mostraron cambios en otros dominios evaluados después del evento FANI, a pesar de que los encuestados informaron de un cambio en sus vidas después del incidente(s) (Mdn 4, Modo 4, DE 1.35; Tabla 5).
Tabla 5. Resultados descriptivos de los cambios tras el incidente de abuso sexual infantil (muestra de testigos) n = 80.
Los FANI tienen fuertes componentes psicológicos que, obviamente, se han descuidado hasta la fecha. Si bien se han realizado y se están realizando grandes esfuerzos para comprender la física de los FANI, se ha prestado muy poca atención a los testigos de los mismos, a la evaluación del impacto psicológico que los FANI tienen en las personas y a sus posibles implicaciones sociológicas. La realidad es una construcción de nuestra mente; nuestro cerebro define lo que entendemos por realidad y la percepción es el mecanismo de aprehensión del reino físico por nuestra mente mediante procesos de transducción. Sin embargo, la percepción individual y las sensaciones previas se malinterpretan con facilidad y la atención -que es el proceso que dirige este conocimiento o procesamiento de la información- también es muy limitada y se distrae o confunde con facilidad, como bien saben los magos. Las limitaciones de nuestros sistemas de atención o capacidades para detectar la realidad han sido estudiadas anteriormente por psicólogos y se ha comparado con los sistemas de inteligencia artificial e incluso con respecto al tema de la investigación SETI (Simons y Chabris, Referencia Simons and Chabris1999; De la Torre y García, Referencia De la Torre and Garcia2018; De la Torre, Referencia De la Torre2020). Los FANI llevan estos procesos a sus límites, a territorios desconocidos, creando disonancia cognitiva en los testigos debido a sus propiedades; las percepciones preformadas y las ideas físicas o existenciales simplemente no encajan. La cognición es el subproducto de procesos descendentes y ascendentes; los primeros son los dominantes en el procesamiento de información nueva, mientras que los segundos están fuertemente arraigados en nuestros recuerdos, experiencias y bancos de conocimientos previos. Los FANI pueden hacer imposible encontrar precedentes en la información preprocesada personalmente, lo que crea una fuerte disonancia interna o un sentimiento de incredulidad que tiene un fuerte impacto en el observador.
En esta investigación, estudiamos el impacto psicológico de los FANI, y los resultados mostraron algunas tendencias y características interesantes. El tema de los FANI parece rondar a diario en la mente de los testigos tras un incidente y fomentar una actitud receptiva hacia ellos. Este efecto puede calificarse de “transformador”, pero centrado específicamente en el fenómeno en sí, ya que no cambia necesariamente otros aspectos de la vida cotidiana del testigo, salvo el conocimiento de los FANI, con un enfoque mayoritariamente no terrestre. Los testigos comparten tendencias en la dirección específica de una especie de pensamiento obsesivo no patológico sobre los FANI, un profundo compromiso mental con los fenómenos tras el suceso. Como hemos mencionado antes, hemos llamado a esta tendencia la tríada del compromiso psicológico profundo con los FANI (UAP-DPET), según lo expuesto anteriormente, pero si este perfil está presente antes del suceso FANI o como consecuencia de la interacción con los fenómenos es algo que queda por dilucidar. Este UAP-DPET en general no tiene un efecto negativo en la vida general del testigo (familia, trabajo o amigos), aunque es claramente algo que hace que el testigo se involucre en actividades relacionadas con el tema, y hay una necesidad de hablar de ello con los demás.
Actualmente se desconoce si esta tríada tiene un correlato neuroanatómico subyacente, ya que no existen estudios relevantes hasta la fecha. En el trastorno obsesivo-compulsivo se han descrito desequilibrios y otras anomalías, tanto neuroanatómicas como en la conectividad entre el putamen y el núcleo caudado (Nakao et al., Referencia Nakao, Okada and Kanba2014; Peng et al., Referencia Peng, He, Ren, Jin, Yang, Xu, Wen, Chen, Wei, Verguts and Chen2022). Resulta pertinente mencionar aquí también que algunas investigaciones recientes también han demostrado la implicación de estas áreas cerebrales en la intuición, los individuos de alto nivel cognitivo (Koch, Referencia Koch2015; Weerasekera et al., Referencia Weerasekera, Ion-M?rgineanu, Green, Mody and Nolan2023), el aprendizaje y la memoria (Foerde y Shohamy, Referencia Foerde and Shohamy2011). La investigación futura podría utilizar una combinación de medidas de evaluación psicológica, neuropsicológica y potencialmente fisiológica, si es posible, determinando si estas tendencias o perfiles psicológicos preexisten o son consecuencias de interactuar con los FANI, con cualquier correlato físico resultante o arrastre en el sistema nervioso humano.
Intereses contrapuestos
Ninguno.
Referencias
Advanced Aerospace Weapon System Applications Contract (AAWSAP) (2007) Available at https://www.dia.mil/FOIA/FOIA-Electronic-Reading-Room/FileId/170018/Google Scholar
Cooper, H, Blumenthal, R and Kean, L (2017) Glowing auras and ‘black money’: the Pentagon’s mysterious UFO program. The New York Times. Available at https://www.nytimes.com/2017/12/16/us/politics/pentagon-program-ufo-harry-reid.htmlGoogle Scholar
Dagnall, N, Drinkwater, K and Parker, A (2011) Alien visitation, extra-terrestrial life, and paranormal beliefs. Journal of Scientific Exploration 25, 699–720. Google Scholar
De la Torre, GG (2020) Does artificial intelligence dream of non-terrestrial techno-signatures? Acta Astronautica 167, 280–285. CrossRefGoogle Scholar
De la Torre, GG and Garcia, MA (2018) The cosmic gorilla effect or the problem of undetected non terrestrial intelligent signals. Acta Astronautica 146, 83–91. CrossRefGoogle Scholar
Escolà-Gascón, Á (2020). Researching unexplained phenomena: empirical-statistical validity and reliability of the multivariable multiaxial suggestibility inventory-2 (MMSI-2). Heliyon 6. Available at https://doi.org/10.1016/j.heliyon.2020.e04291 CrossRefGoogle ScholarPubMed
Foerde, K and Shohamy, D (2011) The role of the basal ganglia in learning and memory: insight from Parkinson’s disease. Neurobiology of Learning and Memory 96, 624–636. CrossRefGoogle ScholarPubMed
Jung, CG (1959) Flying Saucers: A Modern Myth of Things Seen in the Sky. Translated by Hull, R.F.C. Broadway House, London: Routledge & Kegan Paul. Google Scholar
Knuth, KH, Powell, RM and Reali, PA (2019) Estimating flight characteristics of anomalous unidentified aerial vehicles. Entropy 21, 939. CrossRefGoogle Scholar
Koch, C (2015) Intuition may reveal where expertise resides in the brain. Scientific American, 25–26. CrossRefGoogle Scholar
Loeb, A (2022) Overview of the Galileo Project. arXiv preprint arXiv:2209.02479. Google Scholar
Mack, JE (2000) Passport to the Cosmos: Human Transformation and Alien Encounters. Three Rivers Press (CA). Google Scholar
Nakao, T, Okada, K and Kanba, S (2014) Neurobiological model of obsessive–compulsive disorder: evidence from recent neuropsychological and neuroimaging findings. Psychiatry and Clinical Neurosciences 68, 587–605. CrossRefGoogle ScholarPubMed
Olmos, VJB (1994) Alleged experiences inside UFOs: an analysis of abduction reports. Journal of Scientific Exploration 8, 91–105. Google Scholar
Peng, Z, He, T, Ren, P, Jin, L, Yang, Q, Xu, C, Wen, R, Chen, J, Wei, Z, Verguts, T and Chen, Q (2022) Imbalance between the caudate and putamen connectivity in obsessive–compulsive disorder. NeuroImage: Clinical 35, 103083. CrossRefGoogle ScholarPubMed
Project Grudge – Air Force Declassification Office (1949) Available at https://www.secretsdeclassified.af.mil/Portals/67/documents/AFD-110719-005.pdf?ver=2016-07-19-142520-690 (accessed on 10th April 2023). Google Scholar
Project Sign. Report of February (1949). Available at https://web.archive.org/web/20120227085710/http://www.dod.mil/pubs/foi/homeland_defense/UFOs/2d_af_1.pdf (accessed on 9th April 2023). Google Scholar
Ring, K (1993) The omega project. Quill.Google Scholar
Simons, DJ and Chabris, CF (1999) Gorillas in our midst: sustained inattentional blindness for dynamic events. Perception 28, 1059–1074. CrossRefGoogle ScholarPubMed
Swami, V, Pietschnig, J, Stieger, S and Voracek, M (2010) Alien psychology: associations between extraterrestrial beliefs and paranormal ideation, superstitious beliefs, schizotypy, and the Big Five Personality factors. Applied Cognitive Psychology 25, 647–653. CrossRefGoogle Scholar
Teodorani, M (2004) A long-term scientific survey of the Hessdalen phenomenon. Journal of Scientific Exploration 18, 217–251. Google Scholar
Unidentified Flying Objects and Air Force Project Blue Book (1952–1969). Available at https://web.archive.org/web/20030624053806/http://www.af.mil/factsheets/factsheet.asp?fsID=188 (accessed on 9th April 2023). Google Scholar
Weerasekera, A, Ion-M?rgineanu, A, Green, C, Mody, M and Nolan, GP (2023) Predictive models demonstrate age-dependent association of subcortical volumes and cognitive measures. Human Brain Mapping 44, 801–812. CrossRefGoogle ScholarPubMed
Yingling, ME, Yingling, CW and Bell, BA (2023) Faculty perceptions of unidentified aerial phenomena. Humanities and Social Sciences Communications 10, 1–15. https://doi.org/10.1057/s41599-023-01746-3 Google Scholar
10 fenómenos naturales extraños
10 fenómenos naturales extraños
La naturaleza nos deja fenómenos que en ocasiones escapan de la lógica humana, y que a la par poseen una belleza desorbitada. Descubre algunos de los más curiosos.
22 de marzo de 2024
Sarah Romero Periodista científica
Nuestro planeta es el maravilloso escenario de algunos de los fenómenos más desconcertantes e impresionantes que la naturaleza tiene para ofrecer. Desde las preciosas auroras hasta las enigmáticas piedras que se mueven, este tipo de fenómenos naturales de la Tierra despiertan nuestra curiosidad y desafían nuestra comprensión del mundo. Estos sucesos, a menudo raros y fugaces, nos invitan a explorar la insólita interacción de los sistemas de la Tierra y los principios científicos que se esconden detrás de ellos.
Pilares luminosos
Son columnas en posición vertical hacia el cielo, solo visibles cuando la luz se refleja directamente hacia cristales de hielo, ya sea gracias a la luz solar o a través de fuentes artificiales, como luces de la calle o parques. A pesar de su increíble aspecto de columnas de luz sólidas, el efecto visual que proyecta es determinado por nuestro punto de vista relativo.
Las piedras que se mueven solas
Este peculiar fenómeno tiene lugar en EEUU, y se trata de piedras que “flotan” sobre un desierto baldío que antiguamente fue prácticamente fango. Muchos científicos creen que este movimiento es debido al fuerte viento, pero no es del todo convincente para la ciencia, y es que es muy extraño que piedras con tamaño y peso distintos se muevan a un ritmo paralelo y en diferentes direcciones.
Duendes y chorros azules
Estos nombres tan llamativos son adquiridos por ciertos fenómenos que tienen lugar en la atmósfera superior. Catalogados en un principio como OVNIs y con una duración de fracciones de segundo, fueron descubiertos por pilotos de aviones estratosféricos. Los “duendes” son una especie de descargas eléctricas producidas a una altitud de 80 kilómetros con luz rojiza. Por su parte, los “chorros azules”, conos de luz azulada, se forman a menor altura.
Pyrocumulus
Esta curiosa nube cumuliforme es causada mayoritariamente por industrias, fuego, actividad volcánica; en otras palabras, debido al intenso calentamiento del aire desde la superficie. La detonación de armas nucleares también puede producir este tipo de nubes, bajo la forma de hongo nuclear, que es formada por el mismo mecanismo. El aumento de la temperatura da lugar a movimientos que eleva a la masa de aire hasta alcanzar un punto de estabilidad, generalmente en presencia de humedad.
Belt of Venus
El cinturón de Venus ocurre durante las noches polvorientas, cuando una banda de cielo rosado o marrón aparece entre el cielo y el horizonte. El color rosa claro del arco se explica por la retrodispersión de la luz enrojecida a la salida o puesta del Sol.
Círculos de Hielo
Durante su congelamiento, los ríos pueden someterse a sucesos excepcionales. Es lo que ocurre con este fenómeno, producido cuando el hielo de la superficie del río se acumula en mayor grado en el centro que en las orillas, bajo una corriente constante y muy débil. Ésta lo hace girar formando un remolino que, debido a la acción de la fuerza centrífuga, produce finalmente un círculo perfecto de hielo.
Ball Lightning
La conocida en español como “Centella” es menos común y más dañina de lo que se cree. Bajo la apariencia de rayo pero con forma de bola, se mueve con mucha más lentitud que un rayo convencional y puede llegar a medir hasta dos metros y medio de diámetro. Algunos informes revelan que muchas centellas han destruido a su paso edificaciones a lo largo de la historia.
Green Ray
Con una duración de apenas unos minutos, el “Rayo verde” ocurre solamente después del amanecer y antes del ocaso total. Es producido la refracción de la luz en la atmósfera, y se presenta en forma de destello verde por encima del sol.
Dolinas
También conocidas como sumideros, estamos ante uno de los acontecimientos más espantosos de la naturaleza. Con el paso del tiempo, el agua erosiona la tierra bajo la superficie, hasta que en algunas ocasiones, la tierra puede llegar a ceder y acaba hundiéndose en el subsuelo.
Terremoto de Cielo
Dentro de la comunidad científica también es denominado “Cielomoto” o “Skyquake”. Esta explosión emite un sonido que se genera gracias a un movimiento determinado de gases. A falta de una explicación científica concreta hasta el momento, el evento celeste se ha observado en sitios como Florida, Pennsylvania y Australia. En cualquier caso, la teoría más extendida a día de hoy sostiene que el ruido surge al calentarse una capa de aire más que el resto, y al chocar contra el aire más frío tiene lugar una especie de explosión.
Ovnis en Nature
Ovnis en Nature
29 de febrero de 2024
Un artículo en NATURE sobre los FANI es bastante inusual y puede sorprender a algunos miembros de la comunidad científica. Para muchos científicos Nature sigue siendo un referente en cuanto a publicaciones sobre temas fundamentales.
Enlace al texto del artículo: https://www.nature.com/articles/s41598-023-49527-x
He aquí una traducción del resumen del artículo:
“A lo largo de la historia se han registrado avistamientos de objetos voladores no identificados (ovnis) o fenómenos anómalos no identificados (FANI). Dados los riesgos potenciales que suponen para la seguridad y la protección, así como la curiosidad científica, existe un interés creciente por comprender qué representan estos informes de avistamientos. Abordamos este problema como una parte importante de la experiencia humana, que puede examinarse desde una perspectiva geográfica: ¿qué factores locales pueden aumentar o disminuir el número de informes de avistamientos? Mediante un método de regresión bayesiana, comprobamos hipótesis basadas en variables que representan el potencial de observación del cielo (contaminación lumínica, cubierta vegetal y nubosidad) y el potencial de presencia de objetos en el cielo (aeronaves e instalaciones militares).
Cómo entender los agujeros en las nubes
Cómo entender los agujeros en las nubes
30 de enero de 2024
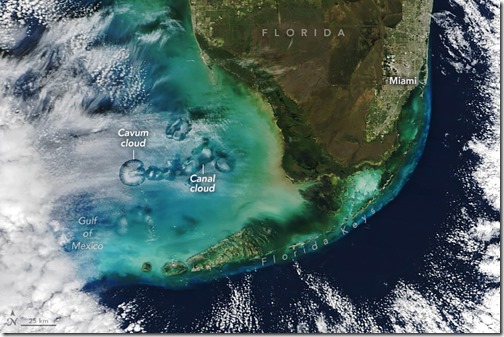 Las nubes Cavum, también denominadas hole-punch clouds (nubes perforadas) o fallstreak holes (agujeros de caída), tienen un aspecto tan extraño que a veces se argumenta que son indicios de platillos volantes u otros fenómenos anómalos no identificados. Vistas desde abajo, pueden parecer como si un gran círculo o elipse hubiera sido recortado limpiamente de las nubes, con mechones de plumas en el centro del agujero.
Las nubes Cavum, también denominadas hole-punch clouds (nubes perforadas) o fallstreak holes (agujeros de caída), tienen un aspecto tan extraño que a veces se argumenta que son indicios de platillos volantes u otros fenómenos anómalos no identificados. Vistas desde abajo, pueden parecer como si un gran círculo o elipse hubiera sido recortado limpiamente de las nubes, con mechones de plumas en el centro del agujero.
Son igualmente impresionantes cuando se ven desde arriba. Esta imagen muestra un grupo de cavum sobre el Golfo de México, frente a la costa oeste de Florida, el 30 de enero de 2024. Fue captada por el MODIS (Moderate Resolution Imaging Spectroradiometer) del satélite Terra de la NASA.
No hacen falta explicaciones de otro mundo para explicar la llamativa formación de nubes. Aunque los científicos han mencionado periódicamente estos fenómenos en revistas científicas y han especulado sobre su causa desde la década de 1940, un par de estudios publicados en 2010 y 2011, dirigidos por científicos de la University Corporation for Atmospheric Research (UCAR), expusieron una explicación que acabó con otras teorías. Las causan los aviones que se desplazan a través de bancos de nubes altocúmulos.
Estas nubes de nivel medio se componen de gotas de agua líquida que se superenfrían; es decir, las gotas permanecen líquidas incluso cuando las temperaturas están por debajo del punto de congelación típico del agua (32 grados Fahrenheit, o 0 grados Celsius). El superenfriamiento se produce cuando las gotas de agua son excepcionalmente puras y carecen de partículas pequeñas, como polvo, esporas de hongos, polen o bacterias, alrededor de las cuales suelen formarse cristales de hielo.
El superenfriamiento puede sonar exótico, pero ocurre de forma rutinaria en la atmósfera terrestre. Los Altocumulus, que cubren aproximadamente el 8% de la superficie terrestre en un momento dado, se componen sobre todo de gotas de agua líquida sobreenfriadas a una temperatura de unos -15 °C. Pero incluso las nubes sobreenfriadas están compuestas por gotas de agua líquida.
Pero incluso las nubes superenfriadas tienen sus límites. A medida que el aire se desplaza alrededor de las alas y las hélices de los aviones, un proceso conocido como expansión adiabática enfría el agua otros 20 °C o más y puede empujar las gotas de agua líquida hasta el punto de congelación sin la ayuda de las partículas suspendidas en el aire. Los cristales de hielo engendran más cristales de hielo a medida que las gotas de líquido siguen congelándose. Los cristales de hielo acaban pesando lo suficiente como para empezar a caer del cielo, dejando un vacío en la capa de nubes. Los cristales de hielo que caen suelen ser visibles en el centro de los agujeros en forma de finas estelas de precipitación que nunca llegan al suelo, lo que se conoce como virga.
A diferencia de otros intentos de explicar el fenómeno, los investigadores de la UCAR, junto con colegas de otras instituciones, como el Centro de Investigación Langley de la NASA, utilizaron una combinación de datos de vuelo de aviones, observaciones por satélite y modelos meteorológicos para explicar cómo se forman las nubes y cuánto duran. Cuando los aviones atravesaban las nubes en un ángulo bastante agudo, los investigadores comprobaron que aparecían pequeños cavum circulares. Si pasaban a través de las nubes en un ángulo poco pronunciado, se hacían visibles “nubes canal” más largas con largas estelas de virga, como la que se muestra arriba.
Otros factores que pueden afectar a la longitud de estas nubes son el grosor de la capa nubosa, la temperatura del aire y el grado de cizalladura horizontal del viento, informaron los investigadores. Su análisis demostró que todo un espectro de tipos de aviones, incluidos los grandes reactores de pasajeros, los reactores regionales, los reactores privados, los reactores militares y los turbohélices, pueden producir nubes cavum y canal. Con más de 1,000 vuelos llegando al Aeropuerto Internacional de Miami cada día, hay muchas oportunidades para que los aviones encuentren las condiciones atmosféricas necesarias para producir nubes cavum.
Imagen del Observatorio de la Tierra de la NASA por Michala Garrison, utilizando datos MODIS de NASA EOSDIS LANCE y GIBS/Worldview. Historia por Adam Voiland.
Los científicos especularon sobre estos agujeros durante décadas, pero ahora se sabe que las nubes cavum son causadas por los aviones.
Imagen del día del 26 de febrero de 2024
Instrumento: Terra – MODIS
Referencias y recursos
· AFP (2023, February 16) Footage of cloud formation misrepresented as UFOs. Accessed February 23, 2024.
· Burrows, S.M. et al. (2022) Ice-Nucleating Particles That Impact Clouds and Climate: Observational and Modeling Research Needs. Reviews of Geophysics, (60)2, e2021RG000745.
· Discover (2014, June 18) The Freaky Physics of Supercooled Water. Accessed February 23, 2024.
· EarthSky (2010, November 7) What are hole-punch clouds, aka fallstreak holes? Accessed February 23, 2024.
· Earth Science Picture of the Day (2008, September 17) Fall Streak and Hole Punch in Florida. Accessed February 23, 2024.
· Heymsfield, A. et al, (2010, June) Aircraft-Induced Hole Punch and Canal Clouds: Inadvertent Cloud Seeding. Bulletin of the American Meteorological Society, 91 (6), 753-766.
· Heymsfield, A. et al, (2011, July 1) Formation and Spread of Aircraft-Induced Holes in Clouds. Science, 333 (6038), 77-81.
· Houston Chronicle (2024, January 11) Notice weird holes open up in the sky over Houston? This is what they are. Accessed February 23, 2024.
· Miami Herald (2024, January 11) Strange hole in clouds over AL stokes talk of ‘mother ship.’ Here’s what it really was. Accessed February 23, 2024.
· National Center for Atmospheric Research (2010, November 7) Mysterious Clouds Produced When Aircraft Inadvertently Cause Rain or Snow. Accessed February 23, 2024.
· NOAA (2020, November 23) “Holey” Clouds Over Michigan Aren’t a Miracle, but a “Supercool” Phenomenon. Accessed February 23, 2024.
· Pedgley, D. (2008) Some thoughts on fallstreak holes. Accessed February 23, 2024.
· Westbrook, C. & Davies, W. Observations of a glaciating hole-punch cloud. Accessed February 23, 2024.
https://earthobservatory.nasa.gov/images/152486/making-sense-of-holes-in-the-clouds